Тепловые и диффузионные процессы при ионном азотировании в тлеющем разряде

При ионном азотировании нагрев обрабатываемой детали происходит за счет бомбардировки поверхности высокоэнергичными ионами насыщающего элемента. При этом температура и скорость нагрева зависят от концентрации ионов насыщающего элемента n_i в при катодной области (или плотности ионного тока j_i) и от разности потенциалов U между электродами.

Проведение моделирования тепловых и диффузионных процессов при ионном азотировании является актульной задачей. Компьютерная модель объединяет в себе описание тепловых и диффузионных процессов.

Для описания температурного поля в модели используется уравнение теплопроводности

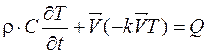, (7.2)

где r– плотность материала, кг/м³;

C – удельная теплоемкость, Дж/(кг·К);

Т – температура, К;

t – время, с;

k – коэффициент теплопроводности,Вт/(м·К);

Q – удельный источник теплоты, Вт/м³.

Вектор теплового потока при передачи тепла теплопроводностью

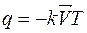. (7.3)

При моделировании используются два различных типа граничных условий: типа Дирихле (граничные условия первого рода) и типа Неймана (граничные условия второго рода). Условие границы типа Дирихле используются, чтобы установить температуру на границе

T = T ₀. (7.4)

Условие типа Неймана используется, чтобы установить поток теплоты на границе

– n·q = q ₀, (7.5)

где q – вектор потока теплоты;

n – нормальный вектор границы;

q ₀ – внутренний поток теплоты, нормаль к границе.

Модуль передачи теплоты «HeatTransfer» в COMSOLMultiphysics использует более общую формулировку уравнения (граничные условия третьего рода)

– n·q = q ₀ + h (T _inf – T), (7.6)

где h – коэффициент теплоотдачи.

Эта формулировка позволяет явно определять поток теплоты через q ₀и коэффициент теплоотдачи h относительно искомой температуры T _inf.

При ионном азотировании, помимо нагрева детали тепловым потоком, происходит одновременный отвод тепла от поверхности в окружающее пространство. Отводом тепла конвекцией и теплопроводностью можно пренебречь, вследствие низкого давления в вакууме. Поэтому, единственным процессом отвода тепла при локальной обработке в вакууме является излучение. Рассмотрим точку x, которая расположена на непрозрачной поверхности с коэффициентом теплового излучения облучаемого тела ε, коэффициентом отражения ρ, с коэффициентом поглощения α и температурой T. Тело не прозрачно. Это означает, что никакая энергия через тело излучением не передается, что является истиной для большинства тел.

Полный излучающий поток теплоты, который достигает элементарной поверхности x, называют падающим тепловым потоком G (рис. 7.5, а).

а) б)

Рис. 7.5. Поступление тепловой энергии G (а), отвод тепловой энергии J (б)

Полный излучающий поток теплоты, который x отдает, называют эффективным потоком J (рис. 7.5, б). Эффективный поток – сумма отраженного излучения и собственного испускаемого излучения

. (7.7)

Поглощенный телом поток теплоты

. (7.8)

Подставляя (7.7) в (7.8) получаем следующее выражение для поглощенного телом потока излучения

. (7.9)

Помимо предположения, что поверхность является непрозрачной, также предполагаем, что поверхность является серой. Для серых поверхностей можем принять следующее

. (7.10)

Подставляем (7.10) в (7.9), убираем коэффициент отражения в уравнении (7.9) и выражаем поглощенный внутрь тела поток излучения q

. (7.11)

Для расчета отвода тепловой энергии излучением от поверхности в окружающее пространство принимаем следующие допущения:

1. Окружающая средаимеет постоянную температуру T_amb.

2. Окружающая среда имеет свойства черного тела, то есть излучаемая и поглощаемая способности тела равны 1, а коэффициент отражения – нулю.

Эти предположения позволяют выразить падающий тепловой поток на поверхность как

. (7.12)

Вставив (7.12) в уравнение (7.11), получим уравнение излучающего потока теплоты от поверхности в окружающее пространство

. (7.13)

Тепловой поток в тлеющем разряде

. (7.14)

где – плотность ионного тока в тлеющем разряде в прикатодной области, мА/см².

U – разность потенциала между электродами, В.

Плотность тока в тлеющем разряде в прикатодной области при ионном азотировании составляет 1-3 мА/см². Известно, что при адсорбции газов, т.е. концентрировании компонентов газовой среды на поверхности, образовывается мономолекулярный адсорбционный слой – монослой. Скорость поступления частиц в адсорбированный слой определяется

, (7.15)

где p – давление в камере, Торр;

Т – температура поверхности, К;

M – молекулярная масса,г/моль.

Для молекулярного азота при температуре Т = 293 Ки давлении р = 1 Торр скорость поступления частиц в адсорбированный слой составляет см^–2с^–1. Если же считать, что полностью сформированный монослой включает 10¹⁵…2·10¹⁵атом/см², то при коэффициенте прилипания, равном единице, время формирования монослоя по порядку величин составит 3·10^–6 с. Таким образом, можно считать, что адсорбированный монослой на обрабатываемой поверхности формируется мгновенно.

Моделирование диффузионных процессов в металле основывается на уравнениях Фика. Первое уравнение (7.16) описывает удельный поток диффундирующего элемента в металле. Знак «минус» означает, что поток направлен из области с большей концентрацией в область с меньшей концентрацией

, (7.16)

где D – коэффициент диффузии, м²/с;

с – концентрация насыщающего элемента, моль/м³;

х – координата, м.

Второе уравнение Фика (7.17) описывает изменение концентрации диффундирующего вещества с (х,τ) в пространстве и во времени. Это уравнение непосредственно следует из уравнения баланса вещества при диффузии и выражения для потока. Оба уравнения описывают одномерную диффузию вдоль оси х

, (7.17)

где τ – время диффузионного насыщения, с.

Для трехмерной диффузии, уравнение диффузии (7.17) принимает вид

, (7.18)

Модуль «TransportofDilutedSpecies» в COMSOLMultiphysics использует граничные условия третьего рода

, (7.19)

где k _м – коэффициент переноса массы, м/с.

Диффузия азота достаточно хорошо описывается теорией надбарьерных перескоков Зинера. Используя уравнение Эйнштейна

, (7.20)

где α – геометрический фактор;

a – параметр решетки;

τ–среднее время между двумя последовательными перескоками внедренного атома.

Применяя для определения величины τ теорию скоростей реакций Эйринга, можно получить выражение для коэффициента диффузии внедренных атомов

, (7.21)

или

, (7.22)

где P – число эквивалентных путей перемещения атома из положения равновесия;

v – частота колебаний атома в положении равновесия вдоль направления диффузии;

Dr – энтропия активации;

Q – теплота активации;

R – универсальная газовая постоянная, Дж/К;

E _a – энергия активации, Дж;

Т – температура, K.

Коэффициент диффузии D определяется свойствами среды и типом диффундирующих частиц.

Коэффициент диффузии азота в α – фазе

. (7.23)

Влияние легирующих элементов на коэффициент диффузии азота учитывается коэффициентом легирования (7.24), при этом коэффициент диффузии азота при легировании одним элементом может быть представлен в виде

, (7.24)

где – коэффициент легирования;

– коэффициент диффузии азота в чистом железе.

При легировании несколькими элементами, коэффициент диффузии азота записывается в виде

. (7.25)

Коэффициент легирования, зависящий от химического состава стали, определяется из выражений

, (7.26)

или

. (7.27)

В зависимости от концентрации легирующих элементов

, (7.28)

где В – постоянный коэффициент.

Далее приведены зависимости коэффициентов легирования от концентрации легирующих элементов (рис. 7.6).

а) б)

Рис. 7.6. Зависимость коэффициентов легирования от концентрации
легирующих элементов при t = 550°C с учетом влияния (а) и без учета
влияния (б) легирующих элементов на растворимость азота в α – фазе

В результате расчетов компьютерной модели было получено распределение температурного поля в детали зубчатое колесо ионном азотировании. На рис.7.7 показано поверхностное распределение температуры детали после 8 часов обработки. При этом температура поверхности зубьев составляла ~550° С.

Из рис.7.7 видно[21], что при установившемся режиме обработки, разность температуры между самыми горячими и холодными участками детали составляет приблизительно 40 K.

Рис. 7.7. Поверхностное распределение температуры
для детали зубчатое колесо при ионном азотировании

На рис.7.8 изображены теоретические кривые 1, 2 изменения температуры T зубчатого колеса в двух крайних точках А и В с течением времени t при ионном азотировании детали.

Рис. 7.8. График нагрева поверхности обрабатываемой детали
в двух крайних точках А и В при ионно азотированиии различных давлениях:
1 – теоретическая кривая (Р =200Па, точка А); 2 – теоретическая кривая (Р =300Па,
точка В); 3 – экспериментальная кривая (точка А); 4 – экспериментальная кривая (точка В)

Из графика (рис. 7.8) видно, что полученные в результате экспериментов зависимости показали хорошее сходство с данными полученными в результате моделирования.

Анализ кривых показывает, что азотируемая поверхность детали нагревается до температуры диффузионного насыщения примерно за 45 минут (скорость нагрева составляет 0,2 K/сек.) после чего температура поверхности остается неизменной до конца обработки. Это связано с установившимся равновесием между подводом тепловой энергии от высокоэнергичных ионов и отводом тепловой энергии излучением от поверхности в окружающее пространство. При этом температура самого «холодного»

Анализ кривых показывает, что азотируемая поверхность детали нагревается до температуры диффузионного насыщения примерно за 45 минут (скорость нагрева составляет 0,2 K/сек.) после чего температура поверхности остается неизменной до конца обработки. Это связано с установившимся равновесием между подводом тепловой энергии от высокоэнергичных ионов и отводом тепловой энергии излучением от поверхности в окружающее пространство [21].

Дата добавления: 2017-02-01