И их числовые характеристики

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Предположим, что некоторая величина X может принимать значения x ₁, x ₂, …, x_n в зависимости от некоторых случайных факторов, так что этим значениям можно сопоставить вероятности p ₁, p ₂, …, p_n. Такая величина называется случайной величиной (СВ). Свои значения СВ принимает случайным образом.

Рассмотрим два основных типа случайных величин: дискретные и непрерывные.

случайная величина называется дискретной, если она принимает отдельные (изолированные) значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или счетным.

случайная величинаназывается непрерывной, если она принимает возможные значения, которые сплошь заполняют некоторый интервал.

Значения функции P (X = x_i) = p_i, i = 1, 2,…, называются рядом распределения вероятностей дискретной случайной величины X.

Законом распределения дискретной случайной величины называется таблица, в верхней строке которой указаны возможные (различные) значения случайной величины X (в порядке возрастания), а в нижней строке под каждым значением x_i – соответствующая вероятность p_i = P (X = x_i), причем .

Все свои значения случайная величина Х принимает с некоторыми вероятностями, используя которые образуют закон распределения для СВ Х:

xi	x 1	x 2	…	xn
pi	p 1	p 2	…	pn

Графически ряд распределения представляется в виде полигона распределения, причем по оси O X откладывают отдельные значения величины X, а по оси O Y – соответствующие им вероятности. Полученные, таким образом точки с координатами (x_i, p_i), где , соединяют прямыми (рис.1).

Интегральной функцией распределения случайной величины X называется функция F (x), выражающая вероятность того, что X примет значение меньшее, чем заданное x:

.

Следствие: .

Рис.1. Полигон распределения

Функция F (x) – неубывающая функция (F (x ₂) ≥ F (x ₁), если x ₂ ≥ x ₁), кроме того, F (–∞) = 0, F (+∞) = 1. Для непрерывной случайной величины функция распределения непрерывна и существует производная , которая называется плотностью распределения вероятностей или дифференциальной функцией распределения. Плотность любой случайной величины неотрицательна и обладает свойствами:

1) ;

2) .

График дифференциальной функции распределения вероятностей называют кривой распределения. Интегральная функция распределения F (x) выражается через функцию плотности f (x) следующим образом:

.

Для непрерывной случайной величины вероятность принятия некоторого конкретного значения P (x = a) = 0. Тогда

    Рис.2. Интегральная функция распределения дискретной случайной величины  

.

Если непрерывная случайная величина , то и (условия нормировки). Для дискретной случайной величины функция распределения кусочно-посто­янна и ступеньки (величины скачков) равны накопленным вероятностям p ₁, p ₁ + p ₂, p ₁ + + p ₂ + p ₃, … (рис.2).

Пример 10. Непрерывная случайнаявеличина X задана функцией распределения:

Найти параметры a и b, плотность и вероятность попадания случайной величины в интервал (1, 5; 3).

Решение. По условиям нормировки имеем F (1) = a+b = 0 и F (2) = 4 a + b = 1, т.е. a = 1/3 и b = –1/3. Тогда функция распределения и ее плотность

Следовательно, получим

P (1,5 < x < 3) = F (3) – F (1,5) = 1 – 1/3(9/4 – 1) = 7/12.

Математическое ожидание или среднее значение случайной величины X есть величина, вычисляемая для дискретной и непрерывной случайных величин по формулам, соответственно:

.

Дисперсия случайной величины X – это математическое ожидание квадрата ее отклонения от ее математического ожидания:

.

Дисперсия для дискретной и непрерывной случайной величин, соответственно

;

.

Среднее квадратичное отклонение случайной величины X обозначим , причем

Пример 11. Пусть заданное распределение имеет вид

xi
pi	0,2	0,3	0,4	0,1

Найти математическое ожидание, дисперсию и среднее квадратичное отклонение.

Решение. Математическое ожидание

= 1 × 0,2 + 3 × 0,3 + 4 × 0,4 + 6 × 0,1 =

= 0,2 + 0,9 + 1,6 + 0,6 = 3,3.

Дисперсия и среднее квадратичное отклонение

= 1×0,2+9×0,3+16×0,4+36×0,1 –

– 3,3² = 0,2+2,7+6,4+3,6-3,3² = 2,01;

.

Пример 12. Для случайной величины X из примера 10 найти среднее квадратичное отклонение.

Решение. Математическое ожидание (см. пример 10)

.

Дисперсия и среднее квадратичное отклонение

.

Дискретная случайная величина X называется распределенной по биномиальному закону, если ее возможные значения равны 0, 1, 2, …, n, а вероятность того, что X = m, выражается формулой Бернулли:

,

где случайная величина X – число появлений некоторого события A в n испытаниях; p – вероятность появления события A в каждом испытании, не изменяющаяся от испытания к испытанию, 0 < p < 1; q – вероятность отсутствия события A в каждом испытании, q = 1 – p.

Математическое ожидание и дисперсия случайной величины X, распределенной по биномиальному закону,

M (X) = np; D (X) = npq.

Дискретная случайная величина X называется распределенной по закону Пуассона, если ее возможные значения равны 0, 1, 2, …, m,…, а вероятность того, что X = m, выражается формулой

где a – параметр закона Пуассона, a > 0.

Как было показано ранее, по этой формуле вычисляются вероятности редких событий, т.е. вероятность появления события A m раз при большом числе испытаний n, в каждом из которых вероятность p появления события A мала (p £ 0,1), однако, произведение np = a постоянно. Математическое ожидание и дисперсия случайной величины X, распределенной по закону Пуассона,

M (X) = a; D (X) = a.

Непрерывная случайная величина X называется равномерно распределенной на отрезке [ a, b ], если ее плотность распределения вероятностей постоянна (т.е. все значения на отрезке случайной величины X равновозможны):

Математическое ожидание и дисперсия СВ, равномерно распределенной на (a, b),

.

Непрерывная случайная величина X называется распределенной по нормальному закону, если ее плотность распределения вероятностей равна:

,

где a – математическое ожидание; s²– дисперсия; s – среднее квадратичное отклонение случайной величины X (a,s – параметры нормального распределения).

Вероятность попадания случайной величины X, распределенной по нормальному закону, в интервал (a, b)

,

где – функция Лапласа.

Вероятность того, что абсолютная величина отклонения меньше постоянного числа , .

Следствие. Правило «трех сигм»: .

Пример 13. Случайная величина X распределена по нормальному закону с параметрами a = 2, s = 5.

Найти вероятность того, что случайная величина X примет значение в интервале (1, 4).

Решение. По условию a = 1,b = 4, a = 2,s = 5. Тогда

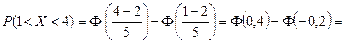
Дата добавления: 2017-02-01