Закон распределения двумерной случайной величины 1 страница

И РЕГРЕССИЯ

СИСТЕМА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН

Система двух случайных величин – совокупность двух случайных величин (X, Y), которые рассматриваются одновременно.

Измерения обычно осуществляются попарно, а полученные значения случайных величин X и Y в определенном смысле взаимосвязаны.

Закон распределения двумерной случайной величины дискретного типа представляет собой перечень значений этой величины и их вероятностей, указанных в специальной таблице. В табл.1 представлены возможные значения (x _i, y_j) и их совместные вероятности:

.

Таблица 1

Y	X
x 1	x 2	…	xi	…	xn	pyj
y 1	p 11	p 21	…	pi 1	…	pn 1	py 1
y 2	p 12	p 22	…	pi 2	…	pn 2	py 2
…	…	…	…	…	…	…	…
yj	p 1 j	p 2 j	…	pij	…	pnj	pyj
…	…	…	…	…	…	…	…
ym	p 1 m	p 2 m	…	pim	…	pnm	pym
pxi	px 1	px 2	…	pxi	…	pxn

Зная закон распределения дискретной двумерной случайной величины (X, Y), можно найти закон распределения каждой случайной величины X и Y:

;

.

Интегральная функция распределения двумерной случайной величины (X, Y) есть вероятность совместного выполнения неравенств X < x и Y < y, т.е.

F (x, y) = P (X < x, Y < y).

Двумерная случайная величина непрерывного типа может быть задана интегральной или дифференциальной функцией распределения. Если интегральная функция распределения всюду непрерывна и имеет непрерывную смешанную частную производную второго порядка, то дифференциальная функция распределения системы двух случайных величин (X, Y) определяется по формуле

.

Плотность распределения отдельных случайных величин, входящих в систему, выражается через плотность системы случайных величин следующим образом:

.

Условный закон распределения случайной величины, входящей в систему, есть закон ее распределения, полученный в предположении, что другая случайная величина приняла определенное значение. Для системы случайных величин дискретного типа условные законы распределения имеют вид

.

Условные математические ожидания (условные средние) дискретных случайных величин

Условные распределения показывают, что одна СВ реагирует на изменение другой изменением своего закона распределения. Такая общая зависимость называется стохастической (вероятностной) и достаточно сложна для изучения. Однако зависимость условного среднего одной СВ от значений другой является функцией, которая называется регрессией: 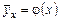– регрессия Y на X, 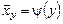– регрессия X на Y. Но и функции регрессии в общем случае достаточно сложны, поэтому используют различные их приближения, например линейной функцией (наилучшей в смысле наименьшего значения среднего квадрата отклонения). Это значит, что для регрессии Y на X функция приближается линейной функцией y = ax + b:

.

Уравнения таких наилучших линейных регрессий

для регрессии Y на X

;

для регрессии X на Y

,

где , , , .

Коэффициент корреляции

характеризует близость (или тесноту) связи между случайными величинами к линейной.

Отметим, что всегда 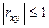. Если , то СВ называются некоррелированными и в этом случае их условные средние значения являются постоянными, т.е. не зависят от значений другой СВ, что характеризует их слабую взаимозависимость. Если (угол между прямыми наилучших линейных регрессий близок к прямому), связь между случайными величинами достаточно слабая и нелинейная. Если (угол близок к нулю), то связь сильная и близка к линейной. В случае промежуточного значения r_xy (и угла) связь достаточно сильна и существенно нелинейная.

5. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Пусть для изучаемой случайной величины X получен ряд ее значений x ₁, x ₂, …, x_n, который называют выборкой объема n из множества всех возможных значений X (генеральной совокупности). Эти значения x_i являются случайными величинами, так как меняются от выборки к выборке.

Важно, чтобы опыты для получения достоверных и правильно представляющих (репрезентативных) генеральную совокупность результатов проводились в одинаковых условиях и независимо друг от друга. Значит, случайные величины x_i будут независимы и одинаково распределены. Согласно центральной предельной теореме (ЦПТ) распределение среднего значения будет приближаться к нормальному распределению при .

Если число n невелико (), то полученные значения можно упорядочить по величине и указать число повторений (частоту) каждого из значений: x ₁ < x ₂ < … < x_k с частотами m ₁, m ₂, …, m_k, где m ₁ + m ₂ + …+ m_k = n (вариационный ряд). При большом числе наблюдений вводятся интервалы группировки , которые охватывают все значения вариационного ряда (причем, первое и последнее значения – с запасом). Интервалы выбираются равными, а их концы возможно более простыми (в целых точках или в целых десятках: 10, 20,…). Обычно удобно ввести не более двух-трех десятков таких интервалов. Например, если x ₁ = 0, …, x_k = 20, то вводим промежутки [–10, 0], [0, 10], [10, 20], [20, 30]. Каждому интервалу сопоставляется его середина x_i и частота m_i, равная сумме частот значений ряда, попадающих в этот интервал. При этом для значения, попавшего на границу двух интервалов, частота делится пополам между ними. Таким образом, составляется сгруппированный вариационный ряд, для которого определяются относительные частоты (или эмпирические вероятности) и эмпирические плотности . По этим данным строятся полигон эмпирического распределения (см. рис.1), гистограмма (рис.3) и эмпирическая функция распределения по накопленной эмпирической вероятности (рис.4).

		Рис.4. Эмпирическая функция распределения
		Рис.3. Гистограмма

По теореме Бернулли (или закону больших чисел) эмпирическая вероятность приближается к теоретической вероятности при , что справедливо и для значений эмпирической функции распределения и гистограммы на интервалах группировки.

По вариационному ряду (в том числе, сгруппированному) вычисляются основные эмпирические или выборочные характеристики: выборочное среднее , выборочная дисперсия и выборочное отклонение :

; ; .

Для каждой выборочной характеристики получается одно определенное значение (точка), которая является приближением соответствующей неизвестной характеристики или случайной величины X. Поэтому эти приближения называют точечными оценками характеристик (или параметров) неизвестного распределения. По закону больших чисел эти точечные оценки сходятся к соответствующим неизвестным значениям: , при , т.е. эти оценки являются состоятельными. Кроме того, выборочное среднее является несмещенной оценкой, т.е. его математическое ожидание (среднее!) равно неизвестному значению : . Выборочная дисперсия является смещенной оценкой: . В результате при небольших объемах (n < 30) часто рассматривают исправленные дисперсию и отклонение вместо и соответственно.

Другой способ оценки неизвестных характеристик или параметров распределения заключается в указании интервала, куда попадает неизвестное значение с заданной вероятностью (или с заданной надежностью):

,

где 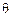– неизвестное значение; – выборочное значение; – надежность (или доверительная вероятность); 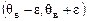– доверительный интервал.

Такие оценки называются интервальными. Например, если распределение X является нормальным с неизвестным и известным параметрами, то радиус интервала , где , и доверительный интервал для a с надежностью

.

Если вместо значения 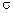, которое может быть неизвестно, использовать точечную оценку , то получим приближенную интервальную оценку с , которая по ЦПТ может применяться и для любого X.

Вероятность задает вероятность ошибки, т.е. того, что значение a не попадает в доверительный интервал.

Отметим, что имеются и другие виды интервальных оценок для этих и других параметров распределения [1, 2].

В случае равноотстоящих друг от друга значений x_i (например, для сгруппированного вариационного ряда) можно упростить вычисления выборочных характеристик, если, выбрав значение (поближе к середине ряда и с большей частотой ), называемое «ложным» нулем, и определив величину шага h для значений ряда, ввести условную варианту по формуле:

.

Тогда значения условной варианты будут целыми числами, причем, большой частоте будет отвечать , и поэтому выборочные характеристики для условной варианты вычисляются проще:

; ;

; .

Обратный пересчет производится по формулам

, , .

При изучении СВ возникает вопрос о возможном виде ее распределения, т.е. о соответствии (согласии) выборочных данных некоторому гипотетическому теоретическому распределению, что является одной из важных задач проверки статистических гипотез.

Основное предположение называется нулевой гипотезой H ₀. Возможно рассмотрение и противоположной (альтернативной) гипотезы или каких-нибудь других гипотез. В нашем случае проверка гипотезы H ₀ состоит в том, что эмпирические данные получены для нормально распределенной генеральной совокупности. Следовательно, при альтернативной гипотезе эмпирические данные не согласуются с ожидаемым нормальным распределением.

Проверка статистических гипотез осуществляется с помощью статистических критериев. Критерий – случайная величина, значение которой вычисляется по эмпирическим данным, т.е. по выборке. Статистический критерий определяет критическую область, при попадании в которую выборочного значения критерия нулевая гипотеза отвергается. Отвергая нулевую гипотезу (если она на самом деле верна), совершают ошибку первого рода; не отвергая нулевую гипотезу (если она на самом деле неверна), допускают ошибку второго рода. Критическая область определяется так, чтобы вероятность ошибки первого рода не превышала уровня значимости 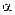, а вероятность совершить ошибку второго рода была бы наименьшей. Обычно в качестве 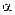берут маленькое число (0,05; 0,01; 0,001; …), при этом следует учитывать, что при будет увеличиваться критическая область, т.е. практически все гипотезы будут отвергаться.

Рассмотрим достаточно простой и эффективный критерий согласия – критерий Пирсона хи-квадрат (), для которого мерой расхождения между эмпирическим распределением (выборкой) и теоретическим распределением является разность между эмпирическими и теоретическими частотами для одного и того же значения дискретной случайной величины или, соответственно, для одного и того же интервала в случае непрерывной случайной величины. Для критерия Пирсона находят величину

,

где m_i – эмпирическая частота; p_i – соответствующая вероятность для теоретического распределения; np_i – теоретическая частота; – объем выборки.

Распределение критерия зависит от числа степеней свободы r и уровня значимости 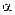. Число r определяется числом значений (или интервалов) k и числом наложенных связей , равным числу соотношений для выборочных данных и теоретических параметров: . Например, так как всегда , то ; если дополнительно положим , то ; если еще положим и (т.е. ), то и т.д. По специальной таблице [2, 3], зная значения r и , находят критическое значение . Вычисленное по выборке значение сравнивают с критическим значением: если , то различие эмпирических данных с теоретическим распределением можно считать несущественным и гипотеза о согласии эмпирических данных с теоретическим распределением не отвергается; если , называемой критической областью, то различия существенны и гипотезу о согласии следует отвергнуть.

Отметим, что при использовании критерия Пирсона значения, частоты которых малы (m_i < 5), можно объединить (обычно это крайние значения или интервалы).

Пример 14. При проведении испытаний материала на разрыв получено 50 значений, характеризующих прочность на разрыв. По этим данным составлен сгруппированный вариационный ряд (масштаб 10⁴ Па).

Интервал D i	120-140	140-160	160-180	180-200	200-220	220-240	240-260	260-280
xi
mi

Оценить согласие полученных данных с нормальным распределением при уровне значимости и получить приближенную интервальную оценку для параметра с надежностью .

Решение. Введем условную варианту, определив шаг h = 20 и выбрав ложный нуль C = 190, и найдем и (табл.2).

Таблица 2

Интервал D i	xi	mi
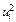
			–3	–6
			–2	–8
Окончание табл.2
Интервал D i	xi	mi
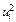
			–1	–10
__________

По данным табл.2 имеем n = 50 и

;

;

Найдем теоретические частоты (табл.3) для интервалов , используя формулу вероятности попадания значений в этот интервал (для нормального распределения с параметрами и ):

.

Таблица 3

D i
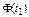
120-140	–2,43	–1,78	–0,4924	0,4624	0,0300	1,5» 1
140-160	–1,78	–1,13	–0,4624	–0,3708	0,0916	4,58» 5
160-180	–1,13	–0,48	–0,3708	–0,1844	0,1864	9,34» 9
180-200	–0,48	0,17	–0,1844	0,0675	0,2519	12,59» 13
200-220	0,17	0,81	0,0675	0,2910	0,2235	11,17» 11
220-240	0,81	1,46	0,2910	0,4279	0,1369	6,87» 7
240-260	1,46	2,11	0,4279	0,4826	0,0547	2,78» 3
260-280	2,11	2,73	0,4826	0,4968	0,0142	0,71» 1

Дата добавления: 2017-02-01