Основные формы задачи ЛП

Задача минимизации ЛП, для которой все ограничения являются равенствами с неотрицательными ресурсами и смысловыми ограничениями, называется канонической задачей.

Каноническая задача имеет вид

,

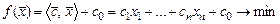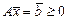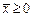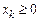, ( и ).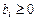

Любую задачу ЛП можно свести к канонической форме, если использовать следующие приемы:

1) 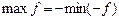, т.е. свести задачу максимизации к задаче минимизации;

2) за счет изменения знака или представления переменной разностью двух новых неотрицательных переменных можно добиться выполнения смысловых ограничений.

если 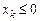, то 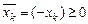, а если знак переменной неизвестен (например, может меняться!), то 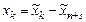, где , ;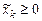

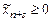3) за счет изменения знака в обеих частях ограничений можно получить все ресурсы ;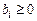

4) за счет прибавления или вычитания в левой части неравенства неотрицательных дополнительных (балансирующих) переменных можно сделать все ограничения равенствами.

Пример 17. Привести к канонической форме задачу ЛП

,

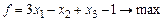Решение. Имеем ;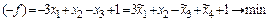

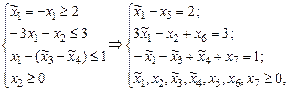
где 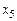, 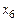и 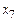– дополнительные (балансирующие) переменные и коэффициенты целевой функции 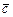= (3, 1, –1, 1, 0, 0, 0), 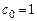. Матрица ограничений

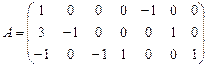
состоит из столбцов коэффициентов ограничений при соответствующих переменных 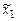, , 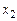, , 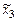, , 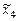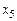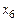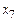; вектор ресурсов .

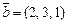Канонические задачи ЛП удобно записывать в виде расширенной матрицы, если представить целевую функцию равенством, аналогичным равенствам ограничений: 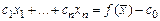и поместить это равенство в дополнительную строку. Таким образом, расширенная матрица канонической задачи ЛП 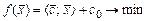, , 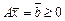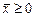имеет вид .

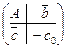В частности, для примера 17 имеем расширенную матрицу

.

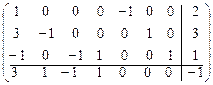Рассмотрим каноническую задачу ЛП в матричном виде. Пусть в матрице ограничений А имеется максимальное число различных столбцов, состоящих из одной единицы и нулей (правильные или базисные столбцы). Такие правильные столбцы линейно независимы и поэтому их число 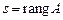. Если элементарными преобразованиями, например методом Гаусса, получить нули под этими правильными столбцами матрицы А и в дополнительной строке расширенной матрицы, т.е. исключить соответствующие переменные из целевой функции (получить правильные столбцы в расширенной матрице), то полученная форма задачи ЛП является правильной или базисной. Таким образом, расширенная матрица правильной задачи, с точностью до перестановки столбцов, имеет вид

,

где 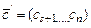, т.е. и 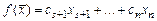. Переменные, соответствующие правильным столбцам, называются базисными (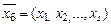), а остальные переменные – свободными (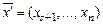). В правильной задаче базисные переменные выражаются через свободные

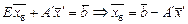, (2)

и в целевую функцию входят только свободные переменные. В правильной задаче ЛП легко выписать начальный допустимый план, если взять свободные переменные равными нулю: 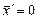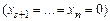. Тогда по (2) 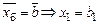, , 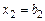…, 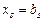. Базисные переменные равны правым частям (ресурсам), стоящим напротив единицы в соответствующем правильном столбце. Таким образом, начальный допустимый план 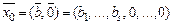. При этом значение целевой функции .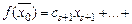

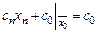Следствие 1. В правильной задаче ЛП ограничения всегда совместны.

Следствие 2. Так как нулевые значения свободных переменных вектора являются крайними, то геометрически начальный допустимый план соответствует некоторой крайней точке симплекса (некоторой его вершине).

Дата добавления: 2017-02-01