Двойственные задачи ЛП

Теорема 3.

Метод искусственного базиса

Для того, чтобы получить правильную форму задачи ЛП без предварительного приведения к ней, используется метод искусственного базиса. В канонической задаче ЛП введем в левую часть уравнений системы ограничений по одной неотрицательной (базисной) искусственной переменной 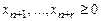с коэффициентом единица так, чтобы матрица ограничений 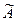для новой задачи стала правильной. Достаточно для этого ввести столько искусственных переменных в уравнения, чтобы число правильных столбцов (с учетом уже бывших в исходной матрице А) стало равно числу уравнений, т.е. строк матрицы А. для переменных 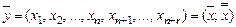, где 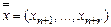– искусственные переменные, составим новую целевую функцию – 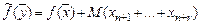, где параметр 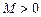должен выбираться достаточно большим по сравнению со всеми величинами, которые могут получиться при конечном числе шагов при решении задачи ЛП. Таким образом, наряду с исходной f -задачей: 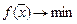, , 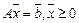сформулирована новая 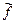-задача: , , .

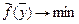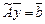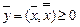Новая задача с искусственными переменными имеет правильную 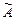матрицу и легко приводится к правильному виду, если исключить базисные переменные из новой целевой функции. Очевидно, если 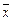– допустимый план f - задачи, следовательно, 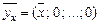– допустимый план для 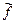-задачи.

1. Если для 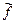-задачи оптимальный план 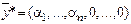, т.е. все искусственные переменные равны нулю, то соответствующий план 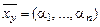будет оптимальным для f - задачи.

2. Если в оптимальном плане 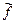-задачи есть искусственные переменные, не равные нулю, то ограничения для f - задачи несовместны (исходная задача неразрешима).

Теорема 4. Если целевая функция 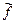-задачи неограниченна снизу (теорема 2, п.2), то f - задача неразрешима.

Пример 21. Для канонической задачи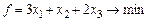

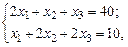
где , , .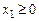

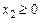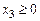Введем искусственные переменные 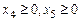. Ограничения и целевая функция теперь имеют вид

.

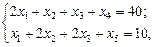
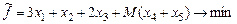Расширенная матрица 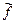-задачи

,

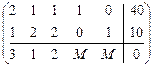
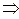
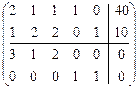где для коэффициентов целевой функции при параметре M введена вторая дополнительная строка. Если в дополнительных строках в каком-то столбце стоят два числа 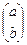, коэффициент при соответствующей переменной в целевой функции равен 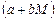. Тогда удобно производить действия с параметром М, вычисляя только коэффициент при этом параметре М, с которым он входит в целевую функцию 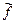-задачи.

Эта задача становится правильной, если исключить базисные (искусственные) переменные 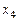и 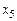из целевой функции:

.

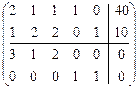
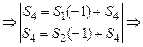
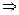
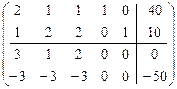Так как большое 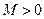, то коэффициенты при свободных переменных 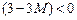, , 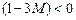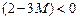и оптимальности нет. Выбирая самый маленький коэффициент 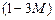, для достижения оптимальности проводим симплексные преобразования:

.

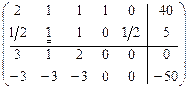
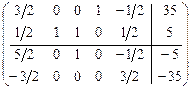
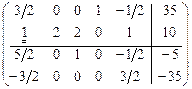
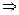
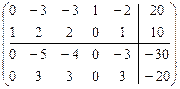Поскольку 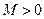, все коэффициенты при свободных переменных 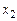, 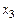и 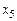целевой функции будут положительны: 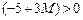, , 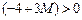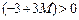. Оптимальность достигнута. Причем оптимальный план один: 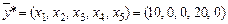и в нем искусственная переменная 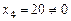. Поэтому по пункту 2 теоремы 3 исходная задача неразрешима (ограничения исходной задачи несовместны). Отметим, что оптимальное значение целевой функции 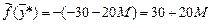содержит параметр М, что свидетельствует об отсутствии оптимального значения у исходной целевой функции.

Пример 22. Решить методом искусственного базиса задачу ЛП:

;

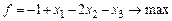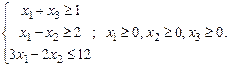
Предварительно приведем задачу к канонической форме, введя балансирующие переменные 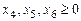и перейдя к минимизации

,

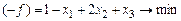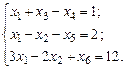
Так как с коэффициентом 1 переменная 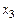входит только в первое уравнение, а переменная 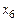– только в третье уравнение, эти переменные могут быть базисными. Введем еще одну искусственную базисную переменную 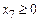во второе уравнение, чтобы матрица 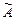стала правильной. Тогда 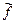-задача имеет вид

;

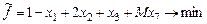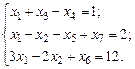
Расширенная матрица этой задачи записывается следующим образом:

.

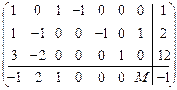
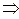
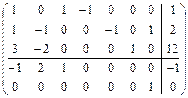
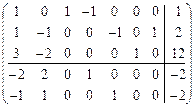Это будет правильная форма 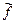-задачи со свободной переменной 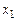, в которой коэффициент целевой функции 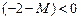(оптимальности нет). Проведем симплексные преобразования:

.

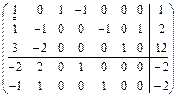
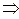
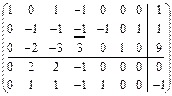
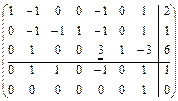
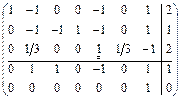
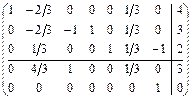коэффициенты при свободных переменных 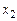, , 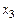, 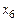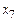в целевой функции положительны и оптимальность достигнута. Оптимальный план один: 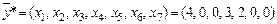. Все искусственные переменные 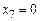. При этом оптимальное значение 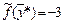и по пункту 1 теоремы 3 оптимальный план 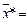(4, 0, 0, 3, 2, 0) Þ 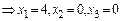и .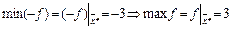

Рассмотрим следующую задачу. Пусть мебельная мастерская производит столы и шкафы из древесины 1, 2 или 3-го сорта. Расход материалов и их запасы следующие:

древесина
на 1 стол	0,15	0,2	0,05
на 1 шкаф	0,3	0,1	0,25
запас, м^3

Цена одного стола 12 условных единиц, а цена одного шкафа 15 условных единиц. Если 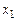– количество производимых столов и 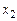– количество производимых шкафов, то план производства 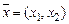и получаем задачу ЛП по оптимизации дохода .

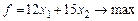в матричном виде

, , ,

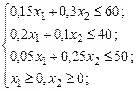
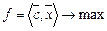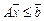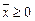где 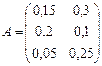, , 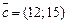, 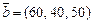она является стандартной задачей ЛП.

Владельцу мастерской предложили продать древесину (без изготовления мебели). Пусть 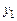, 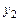и 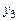– цена 1 м³ древесины соответственно 1, 2 и 3-го сорта. Чтобы продавец не потерял своего дохода от продажи древесины, стоимость древесины, расходуемой на один стол и один шкаф, должна быть не меньше продажной цены древесины этих изделий:

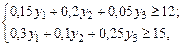(3)

где .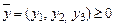

В интересах покупателя стоимость всей древесины необходимо минимизировать:

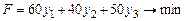. (4)

Таким образом, получили двойственную задачу ЛП (3), (4), в которой максимум заменился на минимум, знаки неравенства изменились на противоположные, столбцы ограничений перешли в соответствующие по порядку строки, правые части ограничений (ресурсы) стали соответствующими по порядку коэффициентами целевой функции и, обратно, коэффициенты целевой функции стали ресурсами, причем число ограничений одной задачи равно числу переменных в другой.

В матричном виде такая взаимная двойственность между задачами ЛП описывается следующим образом:

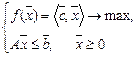
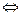
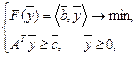
где 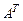– транспонированная матрица А (столбцы становятся на место строк в соответствующем порядке). При этом за счет смысловых ограничений 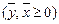выполняются неравенства:

.

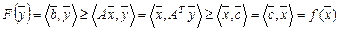Теорема (о минимаксе). Если одна из двойственных задач разрешима, то разрешима и другая, причем экстремальные значения целевых функций обеих задач равны .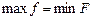

Следствие. Спрос и предложение могут уравновешиваться (возможно равновесие рынка).

Теорема (соотношения двойственности).

1. Если оптимальный план одной из двойственных задач удовлетворяет некоторому ограничению как строгому неравенству, то соответствующая (по номеру ограничения) переменная в оптимальном плане двойственной задачи равна нулю.

2. Если в оптимальном плане двойственной задачи какая-то компонента больше нуля, то соответствующее ограничение исходной задачи выполняется как равенство для ее оптимального плана.

Пример 23. Рассмотрим двойственные задачи ЛП:

;

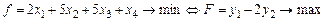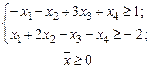
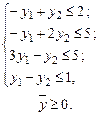
Вторую задачу с двумя переменными легко решить (например, графически на плоскости) и получить оптимальный план 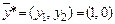. Так как первым трем ограничениям этот план удовлетворяет как строгим неравенствам, то по первому соотношению двойственности в оптимальном плане двойственной задачи (первой задачи) имеем 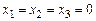. Так как в оптимальном плане 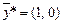второй задачи, двойственной к первой задаче, первая компонента 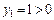, то по второму соотношению двойственности первое ограничение первой задачи выполняется как равенство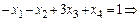 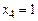. Следовательно, оптимальный план первой задачи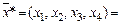 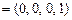и при этом .

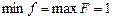Компоненты 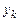оптимального плана 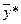двойственной задачи называются оценками (или объективно обусловленными ценами) и по соотношениям двойственности показывают, какие ресурсы 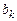исходной задачи исчерпываются, а какие – нет. Кроме того, с помощью этих оценок можно выяснить как изменяется значение целевой функции исходной задачи при изменении ресурсов 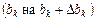. В силу линейности функций

.

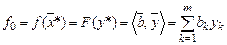Отсюда следует, что .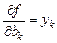

Приращение целевой функции

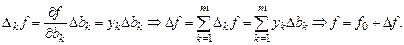
Таким образом, зная оптимальное значение 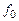, можно определить оптимальное значение и для изменившихся значений ресурсов.

Дата добавления: 2017-02-01