Нечеткие множества

Основы теории нечетких множеств

Программа составлена в соответствии с требованиями образовательного

Материально-техническое обеспечение

1. Учебная аудитория на 200 мест с мультимедийным проектором для проведения лекционных занятий

2. Учебная аудитория на 25 мест с мультимедийным проектором для проведения семинарских занятий

3. Компьютерный класс с доступом в Интернет

стандарта МГУ по направлению подготовки «География»

Разработчик:

Гладкевич Г.И., к.г.н., доцент географического факультета МГУ имени М.В.Ломоносова

Эксперт:

Шувалов В.Е., к.г.н., доцент географического факультета МГУ имени М.В.Ломоносова

Программа одобрена на заседании кафедры экономической и социальной географии России

Протокол №___ от ______20__г.

И. о. заведующего кафедрой проф. Бабурин В. Л. ____________________________

подпись

В системах искусственного интеллекта зачастую приходится иметь дело с нечеткими знаниями, которые нельзя интерпретировать как полностью истинные или полностью ложные. При выводе решения в продукционных системах с нечеткими знаниями требуется решать проблемы представления нечетких знаний и использования их в различных алгоритмах нечеткого вывода.

При попытке формализовать человеческие знания возникла проблема, затруднявшая использование традиционного математического аппарата для их описания. Существует класс описаний, использующих качественные характеристики объектов (много, мало, сильно, слабо, очень сильно и т. п.). Эти характеристики обычно размыты, и их нельзя интерпретировать однозначно. В то же время они содержат важную информацию, например, "Одним из возможных признаков неисправности двигателя является низкое давление масла".

С другой стороны, в системах искусственного интеллекта часто пользуются неточными знаниями, которые нельзя интерпретировать как полностью истинные или полностью ложные. Существуют знания, достоверность которых выражается некоторым коэффициентом, например, 0,5.

Для формального представления таких знаний с учетом свойств их размытости и неточности американским ученым Лотфи Заде предложен математический аппарат нечеткой алгебры и нечеткой логики. Это направление получило широкое распространение, положив начало одной из ветвей теории искусственного интеллекта, именуемой мягкими вычислениями.

Неформально нечеткое множество можно определить как набор элементов произвольной природы, относительно которых нельзя однозначно утверждать, принадлежат ли отдельные элементы этого набора заданному множеству или нет.

Нечеткое множество A, формально определяется как множество упорядочен­ных пар <x, µ_A(x)>, где x есть элемент универсального множества Х, x Î Х, µ_A(x)> — функция принадлежности, принимающая значе­ния на интервале [0, 1]. Эта функция указывает степень принадлежности элемента x нечеткому множеству A.

В частности, значение µ_A{x}=1 означает, что элемент x точно принадлежит нечеткому множеству A, а значение µ_A{x}=0, наоборот указывает на то, что элемент x точно не принадлежит нечеткому множеству A.

Конечные нечеткие множества обычно записывают в виде:

A ={<x₁, µ_A(x₁)>, <x₂, µ_A(x₂)>,…, <x_n, µ_A(x_n)>}.

Кроме того, часто используют и другие варианты задания конечных нечетких множеств, например такой как:

A ={<x₁ /µ_A(x₁)>+<x₂ /µ_A(x₂)>+,…, +<x_n /µ_A(x_n)>}.

Здесь косая черта обозначает разделитель, а символ «+» служит для обозначения теоретико-множественного объединения отдельных элементов.

Пример. Нечеткое множество "юный" можно определить следующим образом:

"юный"={11/0,6 +12/0,8+13/1+14/1+15/0,9+16/0,7+17/0,4+18/0,2}

Такое определение нечеткого множества некоторым экспертом означает, что он с высокой степенью уверенности относит ребенка в возрасте 13-14 лет к юному (µ_A(x)=1). Человека в возрасте 11-12 лет и 15-16 лет также относят к юному с меньшей степени уверенности (0,6≤ µ_A(x)≤0,9), в возрасте 17-18 лет его называют юным достаточно редко. Таким образом, нечеткие множества позволяют учитывать разброс индивидуальных мнений.

Нечеткие множества можно задавать графически. Например, нечеткое множество "юный" графически можно задать, как показано на рис. 1.1 а) и b).

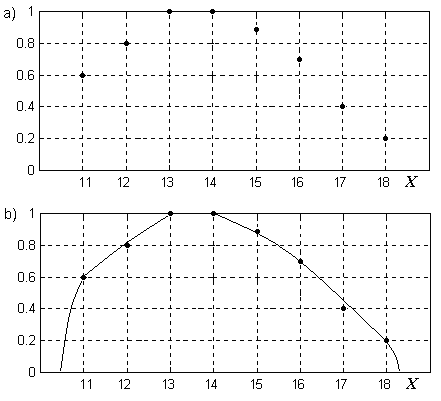
Рис. 1.1. Графическое представление нечеткого множества "юный"

Как видим на рис. 1.1, нечеткое множество можно задать с помощью дискретного (a) или непрерывного (b) графика функции принадлежности m(x).

Дата добавления: 2017-02-01