
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила нечетких продукций
|
|
|
|
Этапы нечеткого вывода
Продукционные системы с нечеткими знаниями
Отметим, что системы искусственного интеллекта, работающие с нечеткими знаниями, чаще всего строятся с использованием продукционной модели представления знаний на основе правил нечетких продукций. Рассмотрим, каким образом осуществляется вывод решений в продукционных системах с нечеткими знаниями.
Чаще всего системы нечеткого вывода используются для управления техническими устройствами и процессами. Разработка и применение систем нечеткого вывода включают в себя ряд этапов.
Информацией, которая поступает на вход системы нечеткого вывода, являются измеренные некоторым образом входные переменные. Они соответствуют переменным процесса управления. Информация на выходе системы нечеткого вывода соответствует выходным переменным, являющимся управляющими переменными процесса управления.
Системы нечеткого вывода выполняют преобразование значений входных переменных процесса управления в выходные переменные на основе нечетких правил продукций. Для этого они должны содержать базу правил нечетких продукций и реализовывать нечеткий вывод заключений на основе посылок или условий, представленных в форме нечетких лингвистических высказываний.
В процессе нечеткого вывода основными являются следующие этапы.
r Формирование базы правил систем нечеткого вывода.
r Введение нечеткости (фаззификация).
r Агрегирование подусловий в нечетких правилах продукций.
r Активизация подзаключений в нечетких правилах продукций.
r Аккумулирование заключений нечетких правил продукций.
r Придание результатам четкости (дефаззификация).
В системах нечеткого вывода условия и заключения отдельных нечетких правил формулируются в форме нечетких высказываний вида 1—3 относительно значений тех или иных лингвистических переменных.
Под правилом нечеткой продукции, или просто нечеткой продукцией, в общем случае понимается выражение вида:
(i): Q; P; A ÞB; S, F, N, (2.1)
где (i) — имя нечеткой продукции; Q — сфера применения нечеткой продукции; P — условие применимости ядра нечеткой продукции; AÞB — ядро нечеткой продукции, в котором A — условие ядра (антецедент); B — заключение ядра (консеквент); "Þ" — знак логической секвенции (или следования); S — метод или способ определения количественного значения степени истинности заключения ядра; F — коэффициент определенности или уверенности нечеткой продукции; N — постусловия продукции.
В качестве имени (i) нечеткой продукции может выступать та или иная совокупность букв или символов, позволяющая однозначным образом идентифицировать нечеткую продукцию в системе нечеткого вывода или базе нечетких правил. В качестве имени нечеткой продукции может использоваться ее номер в системе.
Сфера применения нечеткой продукции Q, условие применимости ядра нечеткой продукции P и постусловие нечеткой продукции N определяются аналогично обычной четкой продукции.
Аналогично обычным правилам продукций ядро AÞB также является центральным компонентом нечеткой продукции. Ядро продукции записывается в форме: "ЕСЛИ A, ТО B" или в распространенном виде: "IF A, THEN B", где A и B — некоторые выражения нечеткой логики, которые часто представляются в форме нечетких высказываний. При этом секвенция интерпретируется в обычном логическом смысле как знак логического следования заключения B из условия A. В качестве выражений A и B могут использоваться составные логические нечеткие высказывания, т. е. элементарные нечеткие высказывания, соединенные нечеткими логические связками, такими как нечеткое отрицание, нечеткая конъюнкция и нечеткая дизъюнкция.
S — метод или способ определения количественного значения степени истинности заключения B на основе известного значения степени истинности условия A. Этот способ в общем случае определяет так схему или алгоритм нечеткого вывода в продукционных нечетких системах и называется также методом композиции или методом активации согласно Стандарту IEC 1131-7. В настоящее время для этой цели предложено несколько способов.
F — коэффициент определенности или уверенности выражает количественную оценку степени истинности или относительный вес нечеткой продукции. Коэффициент уверенности принимает свое значение из интервала [0, 1] и часто называется весовым коэффициентом нечеткого правила продукции.
Простейший вариант правила нечеткой продукции, который наиболее часто используется в системах нечеткого вывода, может быть записан в форме:
ПРАВИЛО <#>: ЕСЛИ "b1 есть a¢", ТО "b2 есть a¢¢". (2.2)
Здесь нечеткое высказывание "b1 есть a¢" представляет собой условие данного правила нечеткой продукции, а нечеткое высказывание "b2 есть a¢¢" — нечеткое заключение данного правила. При этом считается, что b1¹b2.
Запись простейшего варианта правила нечеткой продукции в англоязычной транскрипции:
RULE <#>: IF "b1 IS a¢", THEN "b2 IS a¢¢".
Система нечетких правил продукций, или продукционная нечеткая система, представляет собой согласованное множество отдельных нечетких продукций или правил нечетких продукций в форме "ЕСЛИ A, ТО B" (или в виде: "IF A THEN B"), где A и B — нечеткие лингвистические высказывания вида 1, 2 или 3.
Рассмотрим вариант использования в качестве условия или заключения в некотором правиле нечеткой продукции нечеткого высказывания вида 2, т. е. вида: "b есть Ña", где Ñ — модификатор, определяемый процедурами G и M лингвистической переменной b. Пусть терму a соответствует нечеткое множество . В этом случае исходное нечеткое высказывание "b есть Ña" можно преобразовать к виду 1 в форме нечеткого высказывание "b есть a¢", где терм a¢ получается на основе применения определенной процедурами G и M операции к нечеткому множеству A. Полученное в результате подобной операции нечеткое множество A¢ принимается за значение терм-множества a¢.
Если в качестве условия или заключения используются составные нечеткие высказывания, т. е. образованные из высказываний видов 1 и 2 и нечетких логических операций в форме связок: "И", "ИЛИ", "ЕСЛИ-ТО", "НЕ", то ситуация несколько усложняется. Поскольку вариант использования нечетких высказываний вида 2 сводится к нечетким высказываниям вида 1, то достаточно рассмотреть сложные высказывания, в которых нечеткими логическими операциями соединены только нечеткие высказывания вида 1.
Эта ситуация может соответствовать простейшему случаю, когда нечеткими логическими операциями соединены нечеткие высказывания, относящиеся к одной и той же лингвистической переменной, т. е. в форме: "b есть a¢" ОП "b есть a¢¢", где ОП — некоторая из бинарных операций нечеткой конъюнкции "И" или нечеткой дизъюнкции "ИЛИ".

Нечеткая импликация и нечеткая эквивалентность могут быть выражены через операции нечеткой конъюнкции и нечеткой дизъюнкции, а нечеткое отрицание в здесь является по сути модификатором.
В этом простейшем случае нечеткое высказывание "b есть a¢" И "b есть a¢¢" эквивалентно нечеткому высказыванию "b есть a*", где терм-множеству a* соответствует нечеткое множество A*, равное пересечению нечетких множеств A¢ и A¢¢, которые соответствуют термам a¢ и a¢¢. При этом операция пересечения определяется одним из ранее рассмотренных способов.
Соответственно, нечеткое высказывание "b есть a¢" ИЛИ "b есть a¢¢" эквивалентно нечеткому высказыванию "b есть a*", где терм-множеству a* соответствует нечеткое множество A*, равное объединению нечетких множеств A¢ и A¢¢, которые соответствуют термам a¢ и a¢¢. При этом операция объединения определяется одним из ранее рассмотренных способов.
Пример. Рассмотрим составное нечеткое высказывание вида 3: " скорость автомобиля средняя и скорость автомобиля высокая ". Ему соответствуют два нечетких высказывания первого вида, соединенные логической операцией нечеткой конъюнкции. Тогда исходное нечеткое высказывание эквивалентно нечеткому высказыванию первого вида: " скорость автомобиля средняя и высокая ". Функция принадлежности терма" средняя и высокая " изображена на рис. 2.1 а) более темным фоном, при этом результат нечеткой конъюнкции определялся по формуле (1.3).
а
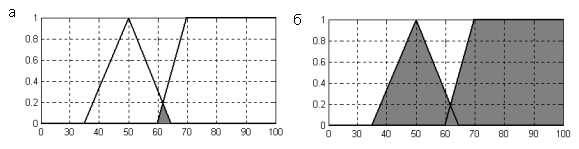
Рис. 2.1. Преобразование составных нечетких высказываний
Рассмотрим аналогичное составное нечеткое высказывание вида 3: " скорость автомобиля средняя или скорость автомобиля высокая ". Ему также соответствуют два нечетких высказывания первого вида, соединенные логической операцией нечеткой дизъюнкции. Тогда исходное нечеткое высказывание эквивалентно нечеткому высказыванию первого вида: " скорость автомобиля средняя или высокая ". Функция принадлежности терма" средняя или высокая " изображена на рис. 2.1 б) более темным фоном, при этом результат нечеткой дизъюнкции определялся по формуле (1.4).
Во-вторых, ситуация может соответствовать более сложному случаю, когда нечеткими логическими операциями соединены нечеткие высказывания, относящиеся к разным лингвистическим переменным в условии правила нечеткой продукции, т. е. в форме: "b1 есть a¢" ОП "b2 есть a¢¢", где ОП — некоторая из бинарных операций нечеткой конъюнкции "И" или нечеткой дизъюнкции "ИЛИ", а b1 иb2 — различные лингвистические переменные.
Этот вариант правил нечетких продукций может быть записан в следующей общей форме:
| или | ПРАВИЛО <#>: ЕСЛИ "b1 есть a¢" И "b2 есть a¢¢" ТО "b3 есть n" ПРАВИЛО <#>: ЕСЛИ "b1 есть a¢" ИЛИ "b2 есть a¢¢" ТО "b3 есть n". | (2.3) |
Здесь нечеткие высказывания: "b1 есть a¢" И "b2 есть a¢¢", "b1 есть a¢" ИЛИ "b2 есть a¢¢"представляют собой условия правил нечетких продукций, а нечеткое высказывание "b3 есть n" — заключение правил. При этом считается, что b1¹b2¹b3, а каждое из нечетких высказываний "b1 есть a¢", "b2 есть a¢¢" называют подусловиями данных правил нечетких продукций.
В случае правил нечетких продукций в форме (2.3) необходимо использовать один из методов агрегирования условий в левой части этих правил.
Наконец, нечеткими логическими операциями могут быть соединены нечеткие высказывания, относящиеся к разным лингвистическим переменным в заключении правила нечеткой продукции, т. е. в форме: "b1 есть a¢" ОП "b2 есть a¢¢", где ОП — некоторая из бинарных операций нечеткой конъюнкции "И" или нечеткой дизъюнкции "ИЛИ", а b1 иb2 — различные лингвистические переменные.
Этот вариант правил нечетких продукций может быть записан в следующей общей форме:
| или | ПРАВИЛО <#>: ЕСЛИ "b1 есть a¢" ТО "b2 есть a¢¢" И "b3 есть n" ПРАВИЛО <#>: ЕСЛИ "b1 есть a¢" ТО "b2 есть a¢¢" ИЛИ "b3 есть n". | (2.4) |
Здесь нечеткое высказывание "b1 есть a¢" представляет собой условие правил нечетких продукций, а нечеткие высказывания: "b2 есть a¢¢" И "b3 есть n", "b2 есть a¢¢" ИЛИ "b3 есть n" — заключения данных правил. При этом считается, что b1¹b2¹b3, а каждое из нечетких высказываний "b2 есть a¢¢", "b3 есть n" называют подзаключениями данного правила нечеткой продукции.
В случае правил нечетких продукций в форме (2.4) необходимо использовать один из методов аккумуляции заключений в правилах нечетких продукций.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 250; Нарушение авторских прав?; Мы поможем в написании вашей работы!