Операции над нечеткими множествами

Подчеркнем, что нечеткие множества являются обобщением обычных четких множеств. Поэтому любое определение некоторой операции над нечеткими множествами должно быть справедливым в случае, когда вместо нечетких множеств используются обычные множества. Для обеспечения возможности сравнения нечетких множеств и выполнения над ними различных операций соответствующие нечеткие множества должны быть определены на одном и том же универсуме.

Прежде всего, определим следующие два простейших отношения между нечеткими множествами.

Равенство. Два нечетких множества A={x, mA(x)} и B={x, m_B(x)} считаются равными (A=B), если их функции принадлежности принимают равные значения на универсуме X:

m_A(x)= m _B (x) для любого xÎX. (1.1)

Нечеткое подмножество. Нечеткое множество A={ x, m_A(x)} является нечетким подмножеством нечеткого множества B={ x, m_B(x)} (обозначают AÍB) тогда и только тогда, когда выполняется следующее условие:

m_A(x)£ m_B(x) (" x Î X). (1.2)

Говорят, что нечеткое множество B доминирует нечеткое множество A, а нечеткое множество A содержится в нечетком множестве B. Нечеткое множество A называют также несобственным подмножеством множества B.

Если в определении нечеткого подмножества исключается равенство соответствующих нечетких множеств, то A называется собственным нечетким подмножеством B и обозначается: AÌ B. При этом нечеткое множество B строго доминирует нечеткое множество A, а нечеткое множество A строго содержится в нечетком множестве B.

Приведем определения нескольких важных логических операций над нечеткими множествами.

Пересечением двух нечетких множеств A и B называют нечеткое множество С (C=AÇB), заданное на этом же универсуме X, функция принадлежности которого определяется по формуле:

m_С(x)= min{m_A(x),m_B(x)} (" x Î X). (1.3)

Пересечение AÇB есть наибольшее нечеткое подмножество C, которое содержится одновременно в нечетких множествах A и B.

Операцию пересечения нечетких множеств называют также min-пересечением или Ù-пересечением (по определению логической операции "И", обозначаемой знаком "Ù").

Объединением двух нечетких множеств A и B называют нечеткое множество С (D=AÈB), заданное на этом же универсуме X, функция принадлежности которого определяется по формуле:

m _D(x)= max{m_A(x),m_B(x)} (" x Î X). (1.4)

Объединение AÈB есть наименьшее нечеткое множество D, которое доминирует одновременно A и B. Операцию объединения нечетких множеств называют max- объединением или Ú-объединением (по определению логической операции "ИЛИ", обозначаемой знаком "Ú").

Заметим, что эта же операция в терминах вероятностного подхода задается в виде:

m _D (x)=m _A(x) + m _B(x) – m_A(x) * m _B (x).

Разностью двух нечетких множеств A и B называется некоторое третье нечеткое множество S (обозначается S=A\B), заданное на этом же универсуме X, функция принадлежности которого определяется по формуле:

m_S(x) = max{m_A(x) - m_B (x), 0} (" x Î X), (1.5)

где используется операция арифметической разности двух чисел.

При построении нечетких моделей сложных систем широко используются унарные операции умножения нечеткого множества на число и возведение нечеткого множества в степень.

Умножение нечеткого множества на число. Пусть A={ x, m_A(x)} — произвольное нечеткое множество, заданное на универсуме X; a — положительное действительное число, такое, что a × h _A £1 (h _A — высота нечеткого множества A). Результат операции умножения нечеткого множества A на число a определяется как нечеткое множество B={ x, m_B(x)}, заданное на этом же универсуме X, функция принадлежности которого определяется по формуле:

m_B(x)= a ×m_A(x) (" x Î X). (1.6)

Эту операцию в дальнейшем будем обозначать через a ×A.

Возведение в степень. Пусть A={ x, m_A(x)} — произвольное нечеткое множество, заданное на универсуме X; k — положительное действительное число. В этом случае формально можно определить операцию возведения нечеткого множества A в степень k как нечеткое множество B={ x, m_B(x)}, заданное на этом же универсуме X, функция принадлежности которого определяется по формуле:

m_B(x) = m_A(x) ^k (" x Î X). (1.7)

Примеры графического представления операции возведения нечеткого множества в степень приведены на рис. 1.2.

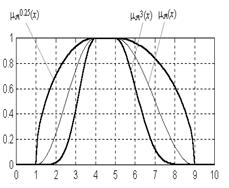
Рис. 1.2. Представление операций возведения в степень

На основе операции возведения в степень определяются две специальные операции над нечеткими множествами: операция концентрирования и операция растяжения нечеткого множества.

Концентрирование. Пусть на универсуме X задано произвольное нечеткое множество A={ x, m_A(x)}. Операция концентрирования, обозначаемая через CON(A), дает в результате нечеткое множество C={ x, m_C(x)}, функция принадлежности которого:

m_C(x) = m_A(x)² (" x Î X). (1.8)

Очевидно, в этом случае CON(A)=A².

Например, для конечного нечеткого множества A={<1, 1.0>, <2, 1.0>, <3, 0.9>, <4, 0.8>, <5, 0.6>, <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>} его концентрирование равно: CON(A)=A²={<1, 1.0>, <2, 1.0>, <3, 0.81>, <4, 0.64>, <5, 0.36>, <6, 0.25>, <7, 0.16>, <8, 0.04>, <9, 0.01>}.

Растяжение. Операция растяжения, обозначаемая через DIL(A), дает в результате нечеткое множество D={ x, m_D(x)}, функция принадлежности которого:

m_D(x) = m_A(x)^0.5 (" x Î X). (1.9)

С помощью операций концентрирования и растяжения выполняется усиление и ослабление лингвистических понятий соответственно. В частности, с помощью операции концентрирования можно задать модификатор «ОЧЕНЬ» для некоторого лингвистического понятия, а с помощью операции растяжения задается модификатор «СРАВНИТЕЛЬНО» или «БОЛЕЕ МЕНЕЕ».

Например, если некоторое понятие, скажем, «старый возраст», определяется как:

A=<x, m_A(x)>, тогда понятие "очень старый возраст" определяется так: CON(A)=A²=<x, m_A(x)²>.

Дата добавления: 2017-02-01