Введение нечеткости

Введение нечеткости (или фаззификация) в продукционную систему нечеткого вывода представляет собой определение значений функции принадлежности нечетких множеств для всех значений входных переменных x_j, входящих в состав предпосылок (подусловий) всех нечетких продукционных правил. При этом x_j Î X_j, где X_j есть универсум лингвистической переменной из j-го подусловия.

Перед началом этапа введения нечеткости некоторым внешним образом, например, с помощью датчиков, задаются значения входных переменных x_j. Причем, эти значения в общем случае могут задаваться как четкие или как нечеткие (с помощью функции принадлежности).
Если значения входных переменных x_j являются четкими, то каждого из них находится количественное значение функции принадлежности µ_Aj(x_j) для каждого из подусловий «b_j есть a_j» в составе базы правил системы нечеткого вывода (j=1,…k). Полученное таким образом значение µ_Aj(x_j) и является результатом введения нечеткости для подусловия «b_j есть a_j». Фактически функция принадлежности µ_Aj(x) задает нам степень истинности подусловия «b_j есть a_j» для j-го правила.

Пример. Рассмотрим пример фаззификации двух нечетких высказываний «температура жидкости небольшая» и «температура жидкости средняя» для входной лингвистической переменной b. Им соответствуют нечеткие высказывания вида: «b есть a₁» и «b есть a₂». Предположим, что температура жидкости составляет 45°, т. е. x_j = 45°. В этом случае фаззификация первого высказывания путем подстановки x₁ = 45° в качестве аргумента функции принадлежности терма a₁ дает нам значение 0 (рис. 2.2 а). Это значение указывает на степень истинности первого высказывания, аналогично получаем, что степень истинности 2-го высказывания составляет примерно 0,72 (рис. 2.2 b).

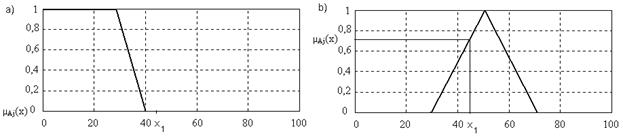
Рис. 2.2. Фаззификация нечетких высказываний по четкому значению

Если значения входных переменных c_j являются нечеткими и задаются с помощью функции принадлежности, то для достижения цели фаззификации применяются операции нечеткой конъюнкции. Чаще всего при этом используются операции min-конъюнкции µ_A’j(x_j) = min{µ_cj (x_j), µ_Aj(x_j)}, "x_j Î X_j или алгебраическое произведение µ_A’j(x_j) = µ_cj (x_j)µ_Aj(x_j)}, "x_j Î X_j.

Пример. Рассмотрим пример фаззификации нечеткого высказывания «температура жидкости небольшая» для входной лингвистической переменной b. Предположим, температура жидкости задается с помощью нечеткой входной переменной c_j, задаваемой с помощью нечеткого множества с функцией принадлежности µ_cj (x_j). В этом случае операция min-конъюнкции дает нам степень истинности высказывания µ_A’j(x_j) равную примерно 0,63 (рис. 2.3 а).

Рис. 2.3. Фаззификация нечеткого высказывания по нечеткому значению

Операция алгебраического произведения дает нам степень истинности высказывания µ_A’j(x_j) равную примерно 0,34 (рис. 2.3 b).

Дата добавления: 2017-02-01