Приведение результатов к четкости

Приведение результатов к четкости, или дефаззификация, представляет собой процесс получения обычного (не нечеткого) значения для каждой из выходных лингвистических переменных множества W ={w₁, w₂,..., w _s }.

При этом, используя результаты аккумуляции всех выходных лингвистических переменных, получают количественное значение каждой из выходных переменных, которое может быть использовано устройствами, внешними по отношению к системе нечеткого вывода.

Этап выполняется следующим образом. Предполагаются известными функции принадлежности всех выходных лингвистических переменных в форме нечетких множеств: X₁¢, X₂¢,…, X _s ¢, где s — общее количество выходных лингвистических переменных в базе правил системы нечеткого вывода. Далее последовательно рассматривается каждая из выходных лингвистических переменных w _j Î W и относящееся к ней нечеткое множество X _j ¢. Результат приведения к четкости для выходной лингвистической переменной w _j определяется в виде количественного значения y_j Î Ñ, получаемого по одной из рассматриваемых ниже формул.

Этап завершается, когда для каждой из выходных лингвистических переменных будут определены итоговые количественные значения в форме некоторого действительного числа, т. е. в виде y ₁, y ₂,..., y_s, где s — общее количество выходных лингвистических переменных в базе правил системы нечеткого вывода.

Для приведения конечных результатов к четкости чаще всего используют следующие методы.

Метод центра тяжести (CoG, Centre of Gravity), или центроид площади, реализуется с помощью формулы:

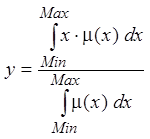, (2.11)

Здесь: y — четкое выходное значение; x — переменная, соответствующая выходной лингвистической переменной w; m(x) — функция принадлежности нечеткого множества, соответствующего выходной переменной w после этапа аккумуляции; Min и Max — левая и правая точки интервала носителя нечеткого множества рассматриваемой выходной переменной w.

При использовании этого метода обычное (четкое) значение выходной переменной равно абсциссе центра тяжести площади, ограниченной графиком кривой функции принадлежности соответствующей выходной переменной.

Пример дефаззификации методом центра тяжести функции принадлежности выходной лингвистической переменной " скорость движения автомобиля " приведен на рис. 2.7. В этом случае имеем y ₁=40 км/ч (приближенное значение).

Рис. 2.7. Пример дефаззификации методом центра тяжести

В случае дискретных функций принадлежности выходной лингвистической переменной ц ентр тяжести рассчитывается по формуле:

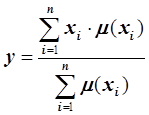, (2.12)

где n — число одноточечных (одноэлементных) нечетких множеств, каждое из которых характеризует единственное значение рассматриваемой выходной лингвистической переменной.

Метод центра площади (CoA, Centre of Area) предполагает, что четкое результирующее значение y определяется из уравнения:

, (2.13)

Центр площади равен абсциссе, которая делит площадь, ограниченную графиком кривой функции принадлежности соответствующей выходной переменной, на две равные части. Метод не может быть использован в случае дискретныхфункцийпринадлежности.

Пример приведения к четкости методом центра площади функции принадлежности выходной лингвистической переменной " скорость движения автомобиля " приведен на рис. 2.8. В этом случае y ₁=35 км/ч (приближенное значение).

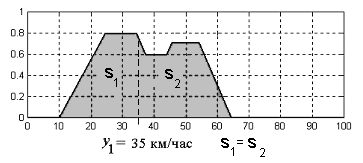
Рис. 2.8. Пример дефаззификации методом центра площади

Метод левого модального значения (LM, Left Most Maximum), или самого левого максимума, предполагает, что расчет проводится по формуле:

, (2.14)

Здесь x_m — модальное значение (мода) нечеткого множества, соответствующего выходной переменной wпосле аккумуляции, рассчитываемое по формуле:

x_m = arg max {m(x)}, x Î [a, b]. (2.15)

Значение выходной переменной определяется как мода нечеткого множества для соответствующей выходной переменной или наименьшая из мод (самая левая), если нечеткое множество имеет несколько модальных значений.

Пример дефаззификации методом левого модального значения функции принадлежности выходной лингвистической переменной " скорость движения автомобиля " изображен на рис. 7.11. В этом случае y ₁= 24 км/ч (приближенное значение).

Рис. 2.9. Пример дефаззификации методом левого модального значения

Метод правого модального значения (RM, Right Most Maximum) или самого правого максимума, предполагает, что расчет проводится по формуле:

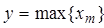, (2.16)

где x_m — модальное значение (мода) нечеткого множества для выходной переменной wпосле аккумуляции, рассчитываемое по формуле (2.15).

В этом случае значение выходной переменной также определяется как мода нечеткого множества для соответствующей выходной переменной или наибольшая из мод (самая правая), если нечеткое множество имеет несколько модальных значений.

Для строго унимодального нечеткого множества левое и правое модальные значения совпадают.

Пример дефаззификации функции принадлежности выходной лингвистической переменной " скорость автомобиля " методом правого модального значения приведен на рис. 2.10. В этом случае y ₁=54 км/ч (приближенное значение).

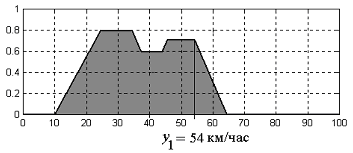
Рис. 2.10. Пример дефаззификации методом правого модального значения

Кроме приведенных методов для приведения результатов к четкости могут быть предложены и другие расчетные формулы. Здесь приводятся лишь те из них, которые нашли наибольшее практическое применение для систем нечеткого вывода.

Дата добавления: 2017-02-01