Алгоритм Сугено (Sugeno)

Алгоритм Цукамото

Алгоритм Цукамото описывается следующим образом (рис. 2.13).

r Формирование базы правил систем нечеткого вывода. Предполагается, что функции m(w_j) (" i Î{1, 2,…, q }) являются монотонными.

r Введение нечеткости для входных переменных.

r Агрегирование подусловий в нечетких правилах продукций. Правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов.

r Активизация подзаключений в нечетких правилах продукций, как и в алгоритме Мамдани, выполняется с помощью min - активизации по формуле (2.5), находятся уровни отсечений c_i. Затем находятся обычные (не нечеткие) значения всех выходных лингвистических переменных в каждом из подзаключений активных правил нечетких продукций. Значение выходной лингвистической переменной w_j в каждом из подзаключений находится как решение уравнения:

c_i = m(w_j) (" i Î{1, 2,…, q }), (2.17)

где q — общее количество подзаключений в базе правил.

r Аккумуляция заключений нечетких правил продукций не требуется, поскольку расчеты осуществляются с обычными действительными числами w_j.

r Дефаззификация выходных переменных выполняется с помощью модифицированного варианта метода центра тяжести для одноточечных множеств:

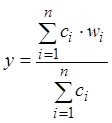, (2.18)

где n — общее количество активных правил нечетких продукций, в подзаключениях которых присутствует выходная лингвистическая переменная w_j.

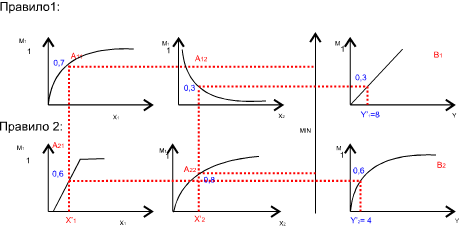
Рис. 2.13. Представление алгоритма Цукамото

Формально алгоритм Сугено, предложенный Сугено и Такаги,может быть определен следующим образом.

r Формирование базы правил систем нечеткого вывода. В базе правил используются только правила нечетких продукций в форме:

ПРАВИЛО <#>: ЕСЛИ "b₁ есть a¢" И "b₂ есть a¢¢" ТО " w = e ₁× a ₁+ e ₂× a ₂". (7.16)

Здесь e ₁, e ₂ — некоторые весовые коэффициенты. При этом значение выходной переменной w в заключении определяется как некоторое действительное число.

r Фаззификация входных переменных. Особенности фаззификации совпадают с рассмотренными выше при описании данного этапа.

r Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий всех правил нечетких продукций, как правило, используется логическая операция min-конъюнкции. Те правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов.

r Активизация подзаключений в нечетких правилах продукций. Во-первых, с использованием метода (7.6) находятся значения степеней истинности всех заключений правил нечетких продукций. Во-вторых, осуществляется расчет обычных (не нечетких) значений выходных переменных каждого правила. Это выполняется с использованием формулы для заключения (7.16), в которую вместо a ₁ и a ₂ подставляются значения входных переменных до этапа фаззификации. Тем самым определяются множество значений C ={ c ₁, c ₂,…, с_n } и множество значений выходных переменных W ={ w ₁, w ₂,..., w_n }, где n — общее количество правил в базе правил.

r Аккумуляция заключений нечетких правил продукций. Фактически отсутствует, поскольку расчеты осуществляются с обычными действительными числами w_j.

r Дефаззификация выходных переменных. Используется модифицированный вариант в форме метода центра тяжести для одноточечных множеств (7.15).

Глава 1. Основы теории нечетких множеств

1. Нечеткие множества
2. Способы[K2] построения нечетких множеств
3. Операции над нечеткими множествами
4. Нечеткие и лингвистические переменные
5. Нечеткие лингвистические высказывания
6. Логические операции с нечеткими высказываниями

Глава 2. Продукционные системы с нечеткими знаниями

1. Этапы нечеткого вывода
2. Формирование [А.Д.3] базы правил систем нечеткого вывода.
3. Введение нечеткости (фаззификация).
4. Агрегирование подусловий в нечетких правилах продукций.
5. Активизация [А.Д.4] подзаключений в нечетких правилах продукций.
6. Аккумулирование заключений нечетких правил продукций.
7. Придание результатам четкости (дефаззификация).
8. Алгоритмы [А.Д.5] нечеткого вывода

[k1]просмотреть и подправить

[K2]Написать, опираясь на Корченкова (сократить)

[А.Д.3]взять пункт 7 из предыдущей главы

[А.Д.4]5-7 см. Леоненкова и Борисова

[А.Д.5]см Борисов и материалы Эл.учебника из Можайки (анимация)

Дата добавления: 2017-02-01