Алгоритм Ларсена

Алгоритм Мамдани

Алгоритмы нечеткого вывода

Рассмотренные этапы нечеткого вывода могут быть реализованы по-разному – с использованием различных подходов на каждом из этапов. Выбор конкретных вариантов параметров каждого из этапов определяет алгоритм нечеткого вывода в системе правил нечетких продукций. В настоящее время наибольшее распространение получили следующие алгоритмы нечеткого вывода.

Алгоритм Мамдани предложен одним из первых для управления паровым двигателем и описывается следующим образом (см. рис. 2.11).

r Формирование базы правил систем нечеткого вывода.

r Введение нечеткости для входных переменных.

r Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий каждого из правил нечетких продукций используются парные нечеткие логические операции. Правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов.

r Активизация подзаключений в нечетких правилах продукций выполняется с помощью min - активизации по формуле (2.5), при этом для сокращения времени вывода учитываются только активные правила нечетких продукций.

r Аккумулирование заключений нечетких правил продукций выполняется с помощью max-объединения по формуле (1.4) для объединения нечетких множеств, соответствующих термам подзаключений, относящихся к одним и тем же выходным лингвистическим переменным.

r Дефаззификация выходных переменных выполняется с использованием метода центра тяжести (2.11)—(2.12) или метод центра площади (2.13).

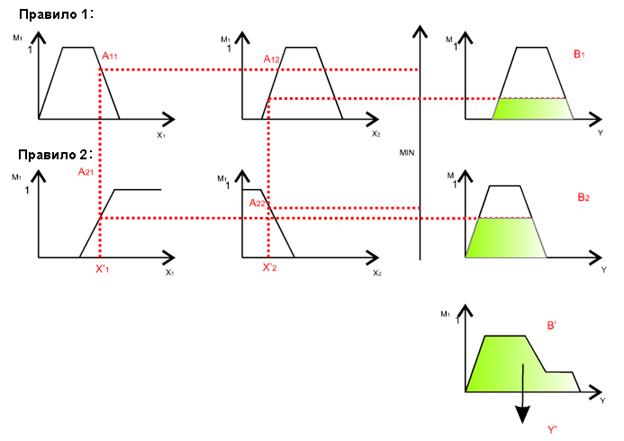
Рис. 2.11. Представление алгоритма Мамдани

Алгоритм [k1] Ларсена описывается следующим образом.

r Формирование базы правил систем нечеткого вывода выполняется аналогично алгоритму Мамдани.

r Фаззификация входных переменных. Особенности фаззификации также совпадают с рассмотренными выше при описании данного этапа.

r Агрегирование подусловий в нечетких правилах продукций. Используются парные нечеткие логические операции для нахождения степени истинности условий всех правил нечетких продукций (как правило, max-дизъюнкция и min-конъюнкция). Те правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов.

r Активизация подзаключений в нечетких правилах продукций. Осуществляется использованием формулы (7.7), посредством чего находится совокупность нечетких множеств: X₁, X₂,…, X _q, где q — общее количество подзаключений в базе правил.

r Аккумуляция заключений нечетких правил продукций. Осуществляется по формуле (3.4) для объединения нечетких множеств, соответствующих термам подзаключений, относящихся к одним и тем же выходным лингвистическим переменным.

r Дефаззификация выходных переменных. Может использоваться любой из рассмотренных выше методов дефаззификации.

Дата добавления: 2017-02-01