Аккумулирование заключений нечетких правил

Аккумулирование заключений нечетких правил в системах нечеткого вывода представляет собой нахождение функции принадлежности для каждой из выходных лингвистических переменных множества W ={w₁, w₂,..., w _s }.

Целью аккумулирования является объединение всех степеней истинности заключений для получения функции принадлежности каждой из выходных переменных. Необходимость выполнения этого этапа обусловлена тем, что подзаключения, относящиеся к одной и той же выходной лингвистической переменной, принадлежат различным правилам системы нечеткого вывода.

Аккумулирование выполняется следующим образом. Предварительно предполагаются известными значения истинности всех подзаключений для каждого из правил R_k, входящих в рассматриваемую базу правил P системы нечеткого вывода, в форме совокупности нечетких множеств: С₁, С₂,…, С _q, где q — общее количество подзаключений в базе правил. Далее последовательно рассматривается каждая из выходных лингвистических переменных w _j Î W и относящиеся к ней нечеткие множества: С _{j 1}, С _{j 2},…, С _jq. Результат аккумуляции для выходной лингвистической переменной w _j определяется как объединение нечетких множеств С _{j 1}, С _{j 2},…, С _jq по одной из формул:

r max-объединение двух нечетких множеств A и B (1.4):

m _D(x)= max{m_A(x),m_B(x)} (" x Î X).

r алгебраическая сумма:

m _D(x)= m_A(x)+m_B(x)- m_A(x)m_B(x), (" x Î X). (2.8)

r граничная сумма:

m _D(x)= min{m_A(x)+m_B(x), 1} (" x Î X). (2.9)

r драстическая сумма:

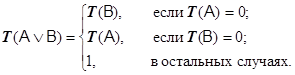
(2.10)

r l-сумма:

m _D(x)= l m_A(x)+(1-l)m_B(x) (" x Î X), lÎ[0, 1]. (2.11)

Этап аккумуляции завершается, когда для каждой из выходных лингвистических переменных будут определены итоговые функции принадлежности нечетких множеств их значений, т. е. совокупность нечетких множеств: С₁¢, С₂¢,…, С _s ¢, где s — общее количество выходных лингвистических переменных в базе правил системы нечеткого вывода.

Пример. Рассмотрим аккумулирование заключений для двух нечетких множеств С₁₁ и С₁₂, полученных в результате выполнения активизации для выходной лингвистической переменной " скорость автомобиля ". Пусть функции принадлежности этих нечетких множеств имеют вид как показано на рис. 2.6, а, б соответственно.

Аккумулирование этих функций принадлежности методом max-объединения нечетких множеств С₁₁ и С₁₂ по формуле (1.4) позволяет получить в результате функцию принадлежности выходной лингвистической переменной " скорость автомобиля ", которая представлена на рис. 2.6, в. Эта функция принадлежности соответствует нечеткому множеству С₁¢, если принять, что рассматриваемая выходная лингвистическая переменная есть w₁.

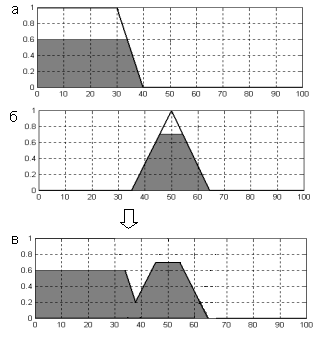
Рис. 2.6. Аккумулирование заключения с использованием max-объединения

Кроме указанных методов для аккумулирования могут использоваться и другие способы, основанные на модификации различных операций объединения нечетких множеств.

Дата добавления: 2017-02-01