Калорические коэффициенты. Энтальпия

Внутренняя энергия простой закрытой системы (система может выполнять только работу расширения) является функцией двух независимых переменных (параметров состояния):

, , .

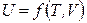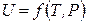Если независимыми переменными выбрать Т и V, то полный дифференциал U запишется

. (2.23)

Подставив значение dU в уравнение первого закона термодинамики

,

получим

. (2.24)

Коэффициенты при независимых переменных в уравнении (2.24) обозначают символам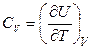и

и ,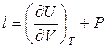

тогда

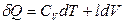. (2.25)

Следовательно, если рассматривать теплоту как функцию температуры и объема, получим:

, . (2.26)

Величины (∂Q / ∂V) _T и (∂Q / ∂T) _V определяются через функцию процесса Q, поэтому без указания конкретных условий проведения процесса их нельзя считать свойствами системы.

Первую из них – (∂Q / ∂V) _T – называют теплотой изотермического расширения; ее размерность совпадает с размерностью давления, и она складывается из внешнего давления Р и члена (∂U / ∂V) _T, который отражает взаимное притяжение молекул и может быть назван внутренним давлением. Этот член мал для реальных газов и очень велик (по сравнению с обычным внешним давлением) для веществ в конденсированном состоянии.

Величина (∂Q / ∂T) _V в соответствии с (2.26) есть теплоемкость при постоянном объеме С_V. Из уравнений (2.23) и (2.26) получим

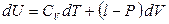(2.27)

где – внутреннее давление.

Как было показано в разделе 2.4, теплота изохорного процесса равна изменению внутренней энергии. Введем новую функцию состояния, изменение которой равно теплоте изобарного процесса.

Определением этой функции служит тождество:

, (2.28)

которое легко получить из первого закона термодинамики в виде

при условии, что работа расширения совершается при постоянном давлении:

. (2.29)

Любая комбинация свойств (функций состояния) является также свойством системы. Поэтому, согласно (2.29), теплота процесса, протекающего при постоянном давлении, равняется изменению функции состояния – энтальпии:

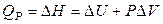. (2.30)

Соотношения (2.29) и (2.30) служат обоснованием основного закона термохимии – закона Гесса.

Из определения энтальпии

H = U + PV

и уравнения первого закона термодинамики для простой системы

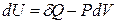
следует, что

,

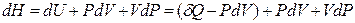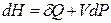. (2.31)

Рассматривая Н как функцию независимых переменных Т и Р

,

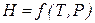получим выражение для дифференциала энтальпии:

. (2.32)

Отсюда получаем

. (2.33)

Коэффициенты при независимых переменных в уравнении (2.33) обозначают символами

и .

Тогда

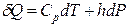. (2.34)

Следовательно, если рассматривать теплоту как функцию температуры и давления, получим:

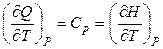и . (2.35)

Величина (∂Q / ∂T) _P в соответствии с (2.35) есть теплоемкость при постоянном давлении С_р. Величину (∂Q / ∂Р) _T называют теплотой изотермического сжатия. Из уравнений (2.32) и (2.35) получим

. (2.36)

Величины l, С_V, C_р, h называются калорическими коэффициентами. Коэффициенты С_V и l определяют зависимость внутренней энергии системы от температуры и объема; а коэффициенты С_р и h – энтальпии от температуры и давления. Теплоемкости С_р и С_V, введенные первоначально как эмпирические коэффициенты, оказались важнейшими термодинамическими параметрами: с их помощью вычисляют изменение термодинамических функций с изменением температуры.

Дата добавления: 2014-01-04