Уравнение адиабаты идеального газа.

В любой термодинамической системе (простой или сложной) могут протекать три процесса: изотермический (Т = const), адиабатический (Q = 0) и политропный (С = const, где C – теплоемкость). В простой системе, в которой внешним параметром является объем V, а сопряженной ему обобщенной силой – давление Р, возможны еще два процесса: изохорный (V = const) и изобарный (Р = const). Эти пять процессов (изотермический, адиабатический, политропный, изохорный, изобарный) считаются основными в термодинамике, причем адиабатический процесс является частным случаем политропного.

Уравнения изохорного, изобарного, изотермического процессов для идеального газа получаются из уравнения состояния PV = RT:

РV = const – уравнение изотермы;

Р = аТ, где а = R / V = const – уравнение изохоры;

V = a ₁ T, a ₁ = R / P = const – уравнение изобары.

Получим уравнение адиабатического расширения (сжатия) идеального газа. Примем, что система совершает только работу расширения и процесс является обратимым (равновесным). Тогда

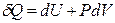
Для идеального газа

,

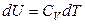следовательно

.

Поскольку процесс адиабатический, то δQ = 0 и, с учетом того, что

, ,

получаем

.

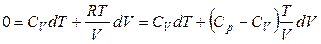Разделим левую и правую часть на (С_V · Т):

,

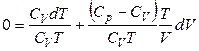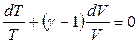, (2.47)

где 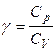– адиабатический коэффициент (g > 1 для любых систем).

Уравнение (2.47) является дифференциальным уравнением адиабаты в переменных Т и V. Проинтегрировав уравнение (2.47) с учетом того, что теплоемкости С_V и С_p (а значит, и адиабатический коэффициент) идеального газа не зависят от температуры и объема, получим:

,

,

(2.48)

Уравнение (2.48) есть уравнение адиабаты идеального газа в переменных Т и V. В переменных P и V уравнение адиабаты принимает вид

, (2.49)

так как

, .

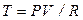И, наконец, уравнение адиабаты в переменных Р и Т имеет вид

, (2.50)

поскольку

, .

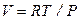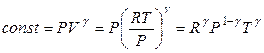Уравнения адиабаты (2.48) – (2.50) называются уравнениями Пуассона.

Теплоемкости одноатомных и двухатомных идеальных газов постоянны и равны:

Идеальный газ	Сp	CV	g
одноатомный
двухатомный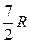

Величину γ для реальных газов можно определить, измеряя скорость звука в газе:

,

где М – молярная масса газа.

Далее, зная величину g, можно, используя в первом приближении уравнение Майера, рассчитать изохорную и изобарную теплоемкость газообразного вещества:

,

, , , .

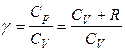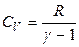При адиабатическом расширении (сжатии) газа Q = 0 и

,

то есть положительная работа совершается за счет убыли внутренней энергии. Следовательно, если идеальный газ адиабатически расширяется (W > 0), то D U < 0 и температура газа уменьшается:

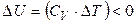только если .

При адиабатическом сжатии температура газа увеличивается. На практике адиабатическим условиям отвечает быстрое (мгновенное) проведение процессов, когда сравнительно медленно протекающий теплообмен мало влияет на изменение внутренней энергии и температуры. Так, при адиабатическом сжатии газа ударной волной газ не успевает отдать выделившуюся теплоту и сильно нагревается.

Используя уравнения адиабат идеального газа, можно получить несколько уравнений для работы равновесного адиабатического процесса. Так как для адиабатического процесса

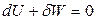
и

,

то

.

Поэтому работа расширения одного моля идеального газа равна

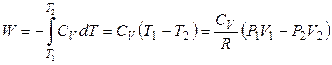, (2.51)

а так как 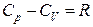и , то

. (2.52)

Следует отметить, что для необратимого адиабатического расширения (сжатия) газа уравнения Пуассона неприменимы. Однако по-прежнему справедливо соотношение

,

а работа необратимого расширения газа против постоянного внешнего давления равна

.

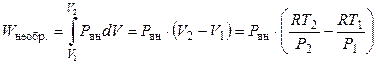Дата добавления: 2014-01-04