Характеристические функции многокомпонентных систем

Термодинамика многокомпонентных систем.

Первый и второй законы термодинамики, из которых следуют фундаментальные уравнения, были получены для закрытых систем (с постоянным числом частиц). При изменении состояния закрытых систем массы компонентов, и, следовательно, состав системы не изменяется. Поэтому термодинамические потенциалы простых закрытых ситем являются функциями только двух переменных:

, (6.1)

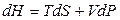, (6.2)

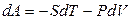, (6.3)

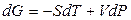. (6.4)

На практике чаще встречаются системы (или части сложной закрытой системы), в которых при протекании различных процессов массы компонентов изменяются. Это может происходить, например, при фазовых превращениях или вследствие протекания химической реакции. При этом может изменяться состав как отдельных частей системы, так и системы в целом.

Поэтому внутренняя энергия (и другие термодинамические потенциалы) открытых систем будут изменяться не только за счет сообщения системе теплоты и произведенной системой работы, но и за счет изменения состава (массы) системы. Для открытых простых систем (без совершения системой полезной работы) характеристические функции будут функциями не только их двух естественных переменных, но и функциями числа молей всех веществ, составляющих систему:

, (6.5)

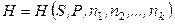, (6.6)

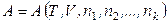, (6.7)

, (6.8)

где n ₁, n ₁, …, n_k – число молей каждого вещества, входящего в систему.

Тогда полный дифференциал внутренней энергии открытой системы можно записать следующим образом:

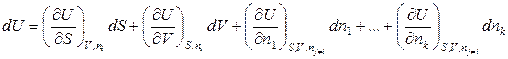, (6.9)

где индекс n_j≠i означает, что число молей других веществ, кроме данного, не изменяется.

Но если открытая система изменяет свое состояние при постоянном составе (все n_i =const), то она ничем не отличается от закрытой системы, поэтому

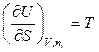и . (6.10)

Следовательно, уравнение (6.9) принимает вид

. (6.11)

Частную производную от внутренней энергии по числу молей i -го компонента при постоянных энтропии, объеме и числах молей всех остальных компонентов Гиббс назвал химическим потенциалом i-го компонента:

. (6.12)

Аналогичным образом можно записать полные дифференциалы других термодинамических потенциалов для открытых систем:

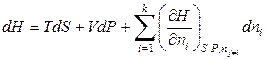, (6.13)

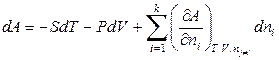, (6.14)

. (6.15)

Далее, для простых систем справедливо:

, , .

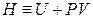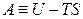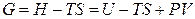Тогда в общем случае

, (6.16)

, (6.17)

. (6.18)

Подставляя в уравнения 6.16 – 6.18 выражение (6.11) с учетом определения химического потенциала

, (6.19)

получаем

, (6.20)

, (6.21)

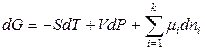. (6.22)

Сравнивая уравнения (6.19 – 6.22) с выражениями для полных дифференциалов термодинамических функций (6.11, 6.13 – 6.15), получаем

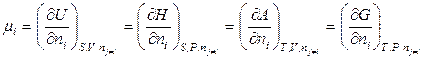, (6.23)

то есть частные производные всех характеристических функций по числу молей i -го компонента при условии постоянства остальных соответствующих переменных равны между собой.

Таким образом, химический потенциал компонента равен приращению характеристической функции системы при добавлении одного моля данного компонента при условии, что естественные переменные и состав остаются постоянными. Сохранить постоянный состав при добавлении одного моля данного компонента можно, если только система достаточно велика.

Следует отметить, что при определении химического потенциала через внутреннюю энергию и энтальпию

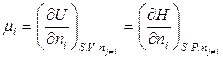
постоянство энтропии системы при изменении массы i -го компонента возможно только при наличии других процессов, компенсирующих изменение энтропии за счет увеличения (уменьшения) количества i -го компонента. Поэтому химический потенциал на практике определяют через частные производные от энергии Гиббса или Гельмгольца. Например,

,

то есть химический потенциал i -го компонента равен изменению энергии Гиббса системы при добавлении бесконечно малого количества этого компонента в систему постоянного состава при постоянных температуре и давлении. Вместо термина «химический потенциал» рассматриваемую частную производную часто называют парциальной молярной энергией Гиббса и обозначают

.

Итак, для простых открытых систем фундаментальное уравнение термодинамики записывается в виде

,

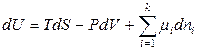где каждое слагаемое можно рассматривать как произведение интенсивного свойства (обобщенной силы) на изменение экстенсивного свойства (обощенной координаты). Поэтому химический потенциал можно считать обобщенной силой, определяющей распределение масс компонентов в системе. Изменение химического потенциала при перераспределении числа молей компонентов приводит к установлению в системе фазового и химического равновесия. По мере протекания процесса химический потенциал компонента выравнивается во всех частях гетерогенной системы. При равновесии химический потенциал компонента одинаков во всех сосуществующих фазах.

Дата добавления: 2014-01-04