Парциальные молярные величины

Пусть состояние простой открытой системы и ее масса задается с помощью набора переменных T, P, n ₁, n ₂, …, n_k. Например, если

, , , ,

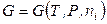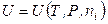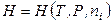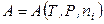то

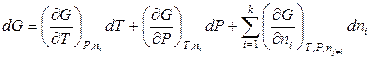, (6.31)

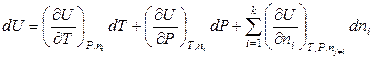, (6.32)

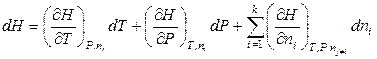, (6.33)

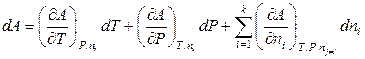. (6.34)

Для энергии Гиббса многокомпонентной системы выражение (6.31), как уже было показано в разделе 6.2, преобразуется к виду

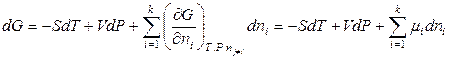, (6.35)

а в изобарно-изотермических условиях справедливо выражение

.

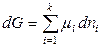В общем случае, если Ф – экстенсивная термодинамическая величина (U, Н, F, G, S, V, C_P, C_V и др.) и

,

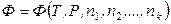то можно определить парциальную молярную величину соотношением

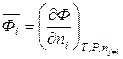. (6.36)

Итак, парциальная молярная величина i-го компонента представляет собой частную производную от экстенсивного свойства системы по количеству i-го компонента при постоянных температуре, давлении и массах остальных компонентов (характеризует изменение функции Ф при добавлении к бесконечно большому количеству системы 1 моля i -го компонента). Следует отметить, что в некоторых учебниках и монографиях применяется термин «парциальная мольная величина», что не соответствует современным требованиям ИЮПАК.

Для чистого вещества (x_i = 1) парциальная молярная величина обращается в молярную величину для индивидуального компонента:

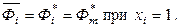
Для многокомпонентных реальных систем парциальные молярные величины i -х компонентов не равны молярным величинам индивидуальных веществ, например:

, , .

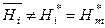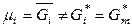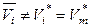С учетом введения новой величины, соотношения (6.31) – (6.34) в изобарно-изотермических условиях (P, T = const) принимают вид:

, (6.37)

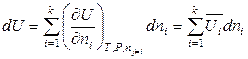, (6.38)

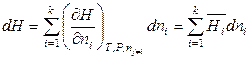, (6.39)

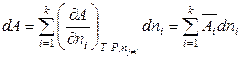. (6.40)

Аналогичные соотношения справедливы и для других экстенсивных величин при P, T = const, например:

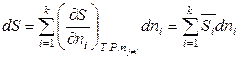. (6.41)

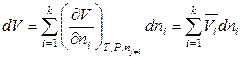. (6.42)

Итак, в общем случае для экстенсивной термодинамической величины в изобарно-изотермических условиях выполняется соотношение

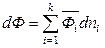. (6.43)

Для энергии Гиббса многокомпонентной системы в изобарно-изо-термических условиях, когда

,

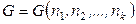согласно определениям химического потенциала и парциальной молярной величины можно записать:

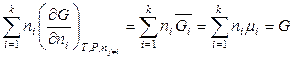. (6.44)

Аналогичные выражения (по теореме Эйлера для однородных функций) справедливы и для других экстенсивных термодинамических свойств при P, T = const (первое уравнение Гиббса-Дюгема):

, , ,

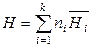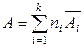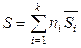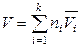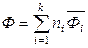, , . (6.45)

В расчете на 1 моль раствора (при делении приведенных выражений на суммарное количество молей всех компонентов) справедливо:

, , , ,

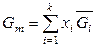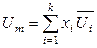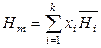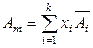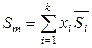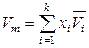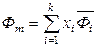, , . (6.46)

Отметим, что согласно определениям химический потенциал i-го компонента есть парциальная молярная энергия Гиббса i-го компонента:

.

Несмотря на то, что химический потенциал может быть определен из нескольких соотношений (6.23):

,

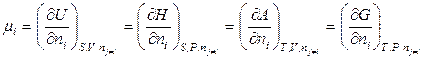только парциальная молярная энергия Гиббса является химическим потенциалом; другие парциальные величины нельзя отождествлять с химическим потенциалом.

Парциальные молярные величины не следует путать и с соответствующими интегральными величинами. Парциальные величины отражают изменение интегрального свойства (определяют вклад данного компонента в общее интегральное свойство системы) и могут принимать значения, нереальные для интегральных величин (например, парциальные молярные объемы могут быть отрицательными и увеличиваться с ростом давления).

Поскольку

,

то второе уравнение Гиббса-Дюгема, полученое для химических потенциалов, будет выполняться и для других парциальных молярных величин, например:

, , ,

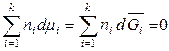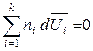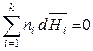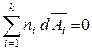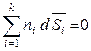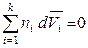, , . (6.47)

Докажем это утверждение. Если Ф – экстенсивная термодинамическая величина и

,

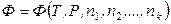то при T, P = const

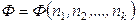
и полный дифференциал Ф запишется как

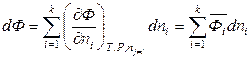. (6.48)

С другой стороны, экстенсивная величина Ф является однородной функцией первого порядка относительно чисел молей компонентов и по теореме Эйлера равна

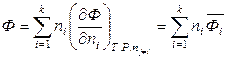. (6.49)

Тогда

. (6.50)

Сравнивая выражения (6.48) и (6.50), получаем обобщенное второе уравнение Гиббса-Дюгема:

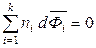. (6.51)

Парциальные молярные величины являются интенсивными параметрами: они зависят не от общего количества, а от относительных количеств всех компонентов (от состава) системы. Парциальные молярные величины определяются также Т и Р.

Парциальные молярные величины в термодинамике растворов имеют такое же значение, как и интегральные молярные величины в термодинамике индивидуальных веществ. Поэтому для компонента в растворе справедливы те же термодинамические соотношения, что и для чистого вещества. Рассмотрим, например, уравнение

,

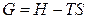где G, H и S относятся к произвольному количеству многокомпонентной системы. При постоянных температуре и давлении справедливо

.

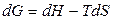Продифференцируем обе части данного выражения по dn_i (числу молей i -го компонента) при условии постоянства давления, температуры и чисел молей всех остальных компонентов системы:

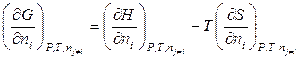, (6.52)

или, с учетом определения парциальной молярной величины (6.36)

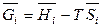. (6.53)

Итак, соотношения между парциальными молярными величинами такие же, как и термодинамические соотношения для чистых компонентов. Например,

,

,

,

.

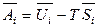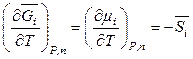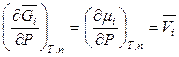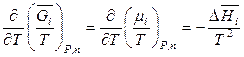Для 1 моль раствора обобщенное уравнение Гиббса-Дюгема (6.51) запишется следующим образом:

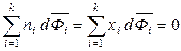, (6.54)

где x_i – мольная доля i -го компонента. Интегрирование уравнения (6.54) при постоянных температуре и давлении позволяет найти зависимость парциальных молярных величин от состава.

Для бинарного раствора в изобарно-изотермических условиях (Р, Т = const), выбрав в качестве независимой переменной x ₂, получим:

,

,

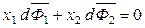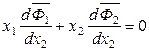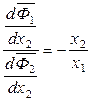. (6.55)

Из уравнения (6.55) следует, что производные 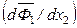и 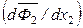всегда имеют противоположные знаки. Если x ₁ = x ₂ = 0,5, то

.

Наклоны кривых 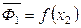и 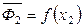отличаются только по знаку: если на одной кривой есть минимум, то на другой кривой при том же составе будет максимум.

Дата добавления: 2014-01-04