Однородные функции состава. Уравнение Гиббса-Дюгема

Итак, полный дифференциал энергии Гиббса простой открытой системы в общем случае равен (6.22)

,

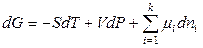а в изобарно-изотермических условиях (P, T = const) –

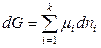. (6.24)

Пусть масса системы изменяется таким образом, что ее состав все время остается постоянным (отношение между массами компонентов остается постоянным). Тогда при интегрировании уравнения (6.24) получим

,

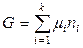. (6.25)

Нижний предел интегрирования соответствует пустой, незаполненной системе (энергия Гиббса равна нулю). Химические потенциалы компонентов оставались постоянными, так как состав системы по мере ее заполнения не изменялся. Химические потенциалы компонентов в изобарно-изотермических условиях являются функцией состава, а не масс компонентов. Уравнение (6.25) можно получить также, используя свойства однородных функций.

Функция многих переменных 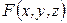называется однородной, если выполняется условие

.

Показатель степени m множителя t носит название показателя однородности.

Характеристические функции (термодинамические потенциалы), а также энтропия и объем являются линейными однородными функциями соответствующих экстенсивных величин (однородными функциями первого порядка, m = 1). Действительно, например, если массы всех компонентов увеличить вдвое, то объем всей системы также увеличится в 2 раза, соответственно в 2 раза увеличатся и другие экстенсивные свойства системы: U, H, A, G, S.

В соответствии с теоремой Эйлера однородные функции обладают следующим свойством:

.

Характеристическая функция энергия Гиббса при постоянных температуре и давлении является линейной однородной функцией только числа молей компонентов

,

тогда по теореме Эйлера

,

,

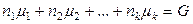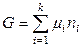. (6.25)

Полученное еще раз уравнение (6.25) называют первым уравнением Гиббса-Дюгема. Для других характеристических функций будет справедливо:

, ;

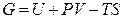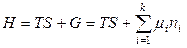, (P = const);

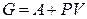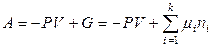, (T = const).

При дифференцировании уравнения (6.25) получаем:

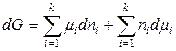. (6.26)

Однако согласно (6.24)

,

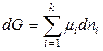тогда

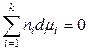. (6.27)

Уравнение (6.27) называется вторым уравнением Гиббса-Дюгема (или просто уравнением Гиббса-Дюгема). Это уравнение часто используется в термодинамике растворов, так как дает возможность рассчитать изменение химического потенциала i -го компонента dμ_i на основе известных изменений химических потенциалов всех остальных компонентов в изобарно-изотермическом процессе.

Для двухкомпонентного (бинарного) раствора уравнение Гиббса-Дюгема принимает вид

. (6.28)

Разделим оба слагаемых на (n ₁ + n ₂):

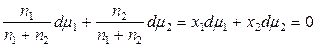, (6.29)

, (6.30)

где x_i – мольная доля i -го компонента в растворе.

Дата добавления: 2014-01-04