Методы расчета парциальных молярных величин

Основой для вычисления парциальных молярных величин служат экспериментальные данные по зависимости экстенсивного параметра системы (раствора) от ее состава. Рассмотрим возможные варианты этих расчетов на примере бинарных растворов.

При проведении опытов можно поступить следующим образом: в изобарно-изотермических условиях последовательно фиксировать некоторые количества растворителя (n ₁) и при каждом выбранном значении n ₁ экспериментально определять значения экстенсивного свойства раствора при различном количестве растворенного вещества (n ₂). Полученные таким образом опытные данные аппроксимируются некоторой эмпирической функцией, диффренцированием которой находят значения парциальных молярных величин. Например, в результате аппроксимации экспериментальных данных получено уравнение

,

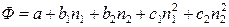где а, b ₁, b ₂, c ₁ и с ₂ – эмпирические коэффициенты. Тогда

, .

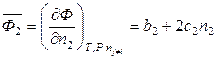Полученные соотношения справедливы и в расчете на 1 моль раствора:

, , .

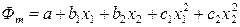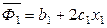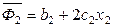Однако чаще на практике экспериментально определяют значения экстенсивного свойства раствора при различном количестве растворенного вещества (n ₂) в постоянном количестве растворителя (n ₁ = const). В этом случае выражения для вычисления парциальных молярных величин несколько усложняются.

Дифференциал интегральной молярной величины в расчете на 1 моль бинарного раствора в изобарно-изотермических условиях согласно (6.43) равен

.

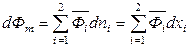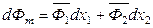. (6.56)

Поскольку

,

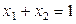то

, ,

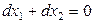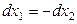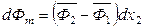, (6.57)

или

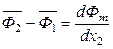, (6.58)

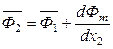. (6.59)

С другой стороны, согласно выражению (6.45)

,

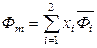поэтому

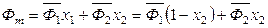. (6.60)

Произведем преобразования (6.60) с учетом (6.58):

,

,

.

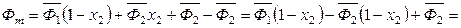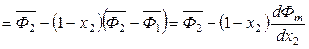Следовательно,

, (6.61)

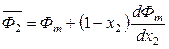. (6.62)

Например, при аппроксимации экспериментальных данных по зависимости молярного объема бинарного раствора от состава (мольной доли растворенного вещества х ₂) было получено уравнение

.

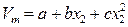Тогда в соответствии с (6.61) и (6.62)

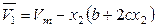и .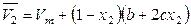

Следует отметить, что при строгой термодинамической записи в выражениях (6.61) и (6.62) должны использоваться не полные, а частные производные при условии постоянства температуры и давления:

, ,

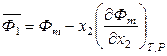однако этим обстоятельством часто пренебрегают как для упрощения формул, так и в связи с тем, что подобная замена допустима в области обычных температур и невысоких давлений.

Если в выражении (6.56)

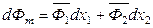
выбрать в качестве независимой переменной х ₁ вместо х ₂ (то есть формально в опытах при неизменном количестве растворенного вещества изменять количество растворителя), то

.

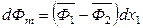Тогда, после преобразований, аналогичных вышеприведенным, можно получить следующие выражения:

. (6.63)

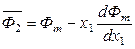, (6.64)

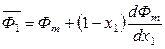. (6.65)

Уравнения (6.61, 6.62, 6.64, 6.65) позволяют определить парциальные молярные величины компонентов на основе известной зависимости интегрального свойства от состава. Например,

, ,

, .

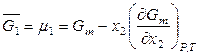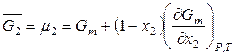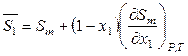На рисунке 6.1 представлена зависимость молярного объема бинарного раствора от состава. В соответствии с уравнениями (6.58), (6.61) и (6.62) можно записать, что

, , .

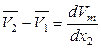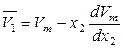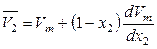Следовательно, отрезки, отсекаемые касательной к кривой V_m = f (x ₂) (для состава точки а) на осях ординат (при x ₂ = 0 и x ₂ = 1), равны значениям парциальных молярных объемов компонентов 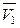и 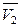соответственно.

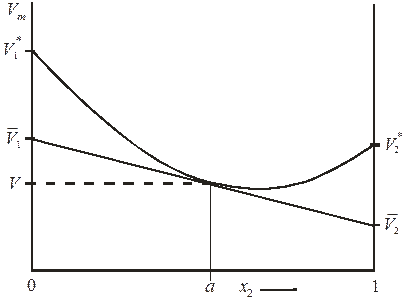
Рис. 6.1. Графическое определение парциальных молярных объемов

компонентов бинарного раствора

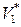(и 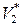– молярные объемы чистых компонентов).

Дата добавления: 2014-01-04