Воднеподібні атоми в квантовій механіці. Квантові числа

7.6.1. З врахуванням виразу (7.3) для потенціальної енергії електрона в кулонівському полі ядра воднеподібного атома, стаціонарне рівняння Шрьодінгера набуде вигляду

. (7.45)

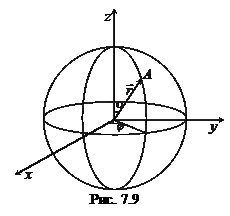Оскільки кулонівське поле володіє центральною симетрією, то зручно перейти до сферичних координат (рис. 7.9), де положення довільної точки А описується трьома координатами 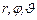. В цьому випадку рівняння Шредінгера набуває вигляду, складнішого від (7.45), але з’являється можливість представити хвильову функцію як добуток радіальної функції R (r) і кутової , тобто провести розділення змінних:

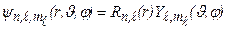. (7.46)

Стандартні вимоги як до хвильової функції в цілому, так і до окремих складових забезпечуються лише при певних, дискретних значеннях не тільки енергії електрона, але і квадрату моменту імпульсу його орбітального руху , а також проекції цього моменту 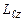на вибраний напрямок (вісь z). Квантування вказаних характеристик визначається трьома квантовими числами: головним n, орбітальним (азимутальним) 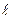та магнітним наступним чином:

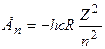, (7.47)

де n =1,2,3,…, тобто співпадає з (7.8) для борівського воднеподібного атома;

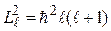, (7.48)

де 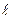= 0,1,2,…, (n- 1);

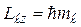, (7.49)

де .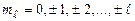

Магнітне квантове число вказує на просторове квантування моменту імпульсу електрона: вектор моменту імпульсу електрона може мати лише такі орієнтації в просторі, що його проекції на вибрану вісь z (яка задається, як правило, напрямком магнітного поля) кратні 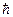(рис. 7.10).

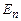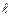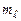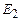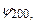
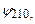
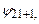
Оскільки енергія електрона визначається лише головним квантовим числом n, а хвильова функція – усіма квантовими числами, то декільком станам з різними та відповідає одне значення енергії. Така ситуація називається квантовомеханічним виродженням. Наприклад, енергія реалізується в чотирьох станах з хвильовими функціями . В загальному, кратність виродження дорівнює . Для ілюстрації приведемо вирази для радіальних і кутових функцій в декількох станах:

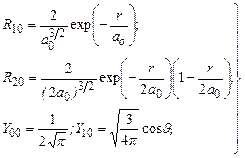(7.50)

де 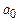– борівський радіус.

Для основного стану (n = 1) хвильова функція має вигляд

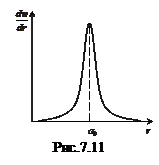
.(7.51)

Імовірність знайти електрон в сферичному шарі товщиною dr, тобто в елементарному об’ємі 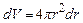, становить

а в шарі одиничної товщини –

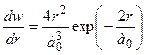. (7.52)

Як видно з рис. 7.11, залежність 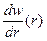володіє різким максимумом при r = а ₀. Отже, борівська орбіта в квантовій механіці може інтерпретуватись як геометричне місце точок, де імовірність перебування електрона – максимальна. Але, оскільки заряд електрона “розмазаний” по усьому атомі 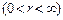, то в квантовій механіці, у відповідності зі співвідношенням невизначеностей Гайзенберга, поняття орбіти (траєкторії) електрона втрачає зміст.

7.6.2. Стани електрона з різними значеннями орбітального квантового числа 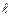прийнято позначати наступним чином:

						.
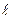
Стан	s	p	d	f	g

Тому енергетичні рівні з різними n реалізуються наступними станами:

n = 1 –	стан	1 s;
n = 2 –	стани	2 s,	2 p;
n = 3 –	стани	3 s,	3 p,	3 d;
n = 4 –	стани	4 s,	4 p,	4 d,	4 f.

Стан 1 s є основним, усі інші стани – збуджені. Час життя електрона в збудженому стані складає ~.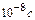

Енергетична діаграма квантовомеханічного атома водню має вигляд (рис.7.12), який дещо відрізняється від діаграми борівського атома (рис.7.4). Як і раніше, квантова механіка не накладає жодного обмеження на зміну головного квантового числа. В цей же час зміна 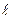і 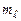регламентується правилами відбору

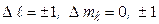. (7.53)

Друге правило відбору тут не проявляється, але стає важливим, коли випромінюючі атоми перебувають в магнітному полі.

Дата добавления: 2014-01-04