Состав насыщенного пара идеального жидкого раствора

Насыщенный пар над жидким раствором, все компоненты которого летучи (обладают измеримым парциальным давлением пара), содержит те же компоненты, что и жидкий раствор. Рассмотрим бинарный жидкий идеальный раствор: обозначим через x ₁ мольную долю растворителя в жидком растворе, через х ₂ = (1 – х ₁) – мольную долю растворенного вещества в жидком растворе; через y ₁ – мольную долю растворителя в насыщенном паре, через y ₂ = (1 – y ₁) – мольную долю растворенного вещества в насыщенном паре.

Общее давление насыщенного пара над идеальным раствором равно сумме парциальных давлений компонентов:

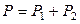, (8.16)

причем по закону Рауля для идеального раствора

,

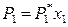а по закону Генри для идеального раствора

.

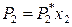Следовательно, зависимость общего давления насыщенного пара над бинарным идеальным жидким раствором от состава раствора определяется следующим уравнением:

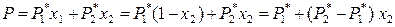. (8.17)

Таким образом, парциальные давления пара компонентов и общее давление насыщенного пара идеального жидкого раствора являются линейными функциями состава раствора (рис. 8.1).

Рис. 8.1. Зависимость парциальных давлений пара компонентов и общего

давления насыщенного пара от состава идеального жидкого раствора.

Найдем связь между составом жидкого раствора и составом насыщенного пара, который будем считать идеальной газовой смесью. По закону Дальтона мольная доля растворенного вещества в паре равна

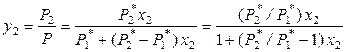. (8.18)

Введем новую величину – относительную летучесть, равную

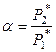. (8.19)

Тогда

. (8.20)

Из уравнения (8.20) видно, что состав насыщенного пара не совпадает с составом идеального жидкого раствора: в общем случае y ₂ ≠ x ₂. Составы совпадают только в тех случаях, кода либо α = 1 (давления насыщенного пара чистых компонентов при данной температуре равны), либо x ₂ = 1 (чистый растворенный компонент).

Соотношение между составом идеального жидкого раствора и составом насыщенного пара можно изобразить графически (рис. 8.2), если по оси ординат откладывать состав пара y, а по оси абсцисс – состав раствора x. Видно, что чем больше α отличается от единицы, тем больше состав пара отличается от состава жидкого раствора.

Рис. 8.2. Зависимость состава насыщенного пара от состава жидкого

идеального раствора при различных значениях относительной летучести.

Более того, при α > 1 в насыщенном паре содержится больше растворенного вещества, чем растворителя, а при α < 1 насыщенный пар над раствором обогащен растворителем. Так, например, из уравнения (8.20) при фиксированном составе жидкого раствора x ₂ = 0,50 получаем:

если α = 1, то y ₂ = 0,50; если α = 2, то y ₂ = 0,67;

если α = 3, то y ₂ = 0,75; если α = 0,5, то y ₂ = 0,33.

Найдем также зависимость общего давления насыщенного пара над идеальным жидким раствором от состава пара при постоянной температуре. Из уравнения (8.20) следует, что

,

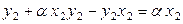. (8.21)

Подставив соотношение (8.21) в уравнение (8.17), получим:

. (8.22)

Поскольку

,

то

,

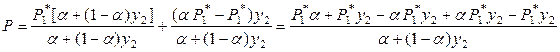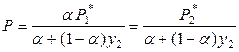. (8.23)

Таким образом, общее давление насыщенного пара над идеальным жидким раствором не является линейной функцией состава пара. Кривизна функции Р = f (y) будет возрастать с увеличением относительной летучести компонентов α. При α = 1 согласно (8.23)

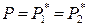
во всей области составов жидкого раствора.

8.4. Диаграммы равновесия «жидкость – пар» идеальных бинарных растворов. Правило рычага.

Диаграмма равновесия (диаграмма состояния, фазовая диаграмма) – это геометрическое изображение в пространстве или на плоскости равновесных состояний термодинамической системы при различных значениях параметров, определяющих эти состояния: температуры, давления, состава системы и т.д. (Диаграммой состояния называется график, выражающий зависимость равновесного состояния системы от внешних условий или от состава системы).

Диаграммы равновесия бинарных систем изображают области существования их различных фаз. При построении диаграмм состояния двухкомпонентных систем обычно принимают постоянными давление или температуру, что позволяет вместо объемных диаграмм в координатах «давление – температура – состав» рассматривать их сечения плоскостью P = const или T = const. Так получают диаграммы равновесия (состояния) «давление – состав» при постоянной температуре и «температура – состав» при постоянном давлении.

Вначале рассмотрим диаграммы «давление насыщенного пара – состав раствора» при постоянной температуре при условии, что жидкий раствор является идеальным и насыщенный пар представляет собой смесь идеальных газов. Указанная диаграмма легко получается, если в координатах «давление – состав» при T = const построить зависимость давления насыщенного пара от состава раствора и состава пара (рис. 8.3). Действительно, общее давление насыщенного пара над раствором в зависимости от состава жидкого раствора описывается уравнением (8.17)

,

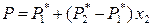а в зависимости от состава пара – уравнением (8.23):

. (8.23)

Любая точка на диаграмме равновесия (состояния) называется фигуративной точкой и характеризует общий состав системы и какое-либо ее свойство (в данном случае давление насыщенного пара). Если фигуративная точка расположена в области существования одной фазы, то она называется фигуративной точкой фазы, а если в области существования гетерогенной системы – то фигуративной точкой системы.

Рис. 8.3. Зависимость общего давления насыщенного пара

от состава идеального жидкого раствора и от состава пара.

На диаграмме состояния присутствуют две линии: верхняя кривая (прямая линия) отображает зависимость давления насыщенного пара от состава жидкого раствора и назывется линией жидкости, нижняя кривая (выпуклая вниз кривая) отображает зависимость давления насыщенного пара от состава пара и называется линией пара. Этими линиями плоскость диаграммы делится на три поля.

Верхнее поле (область I) охватывает значения давлений P и составы х, при которых существует только одна фаза – жидкий раствор. В этой области давления больше давлений насыщенного пара при данной температуре. Нижнее поле (область II) соответствует пару (газовой смеси) переменного состава. В этой области давления газа меньше давления насыщенного пара при данной температуре.

Среднее поле (область III), заключенное между линиями жидкости и пара, соответствует равновесной двухфазной системе, состоящей из двух фаз – жидкого раствора и насыщенного пара. В этой области жидкая и паровая фазы сосуществуют и находятся в равновесии. Состав фаз определяется координатами точек, лежащих на пересечении изобары ba, которая проходит через фигуративную точку системы k, с линиями жидкости и пара. Точка a характеризует состав жидкого раствора, точка b – состав насыщенного пара, который находится в равновесии с раствором состава a. Фигуративная точка системы k характеризует общий (валовый) состав системы.

Следует отметить еще раз, что даже в случае образования идеальных растворов состав пара не совпадает с составом жидкого раствора. Так, парциальное давление пара растворителя по законам Рауля и Дальтона равно

.

Тогда

.

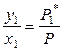Для случая, представленного на рис. 8.3, давление пара над чистым растворителем всегда больше общего давления насыщенного пара над раствором, поэтому y ₁ > x ₁ во всей области концентраций. Пар обогащен растворителем по сравнению с жидким раствором.

Количества (массы) фаз, находящихся в равновесии, могут быть определены на диаграммах состояния по правилу рычага. Пусть общее количество веществ в бинарной системе равно 1 моль, а общий состав системы характеризуется значением x ₀. На диаграмме состояния Р – х (рис. 8.3) состоянию системы соответствует точка k, а состояниям жидкой и паровой фаз – точки a и b соответственно. Мольная доля растворенного вещества в растворе – х ₂, в насыщенном паре – y ₂. Обозначим массу пара (в молях) через m, тогда масса раствора равна (1 – m). Составим уравнение материального баланса: общее количество молей растворенного вещества равно сумме его количеств в жидкости и паре:

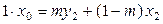. (8.24)

Вычтем из левой и правой части уравнения (8.24) х ₂ и преобразуем полученное выражение:

,

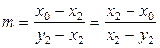. (8.25)

Теперь вычтем из левой и правой части уравнения (8.24) y ₂:

,

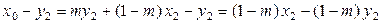. (8.26)

Разделим уравнение (8.25) на (8.26), получим:

. (8.27)

Разности (х ₂ – х ₀) и (х ₀ – y ₂) равны отрезкам ka и bk, на которые точка k делит прямую ba, соединяющую составы фаз, находящихся в равновесии. Значит,

.

Итак, получаем правило рычага: массы (количества) находящихся в равновесии фаз обратно пропорциональны отрезкам, на которые фигуративная точка системы делит прямую, соединяющую фигуративные точки фаз. Если уравнение (8.27) записать в виде

,

то полученное равенство представляет условие равновесия рычага. Правило рычага выполяется при гетерогенных равновесиях как для идеальных, так и реальных растворов.

Дата добавления: 2014-01-04