Температура кипения идеального раствора

Диаграмма состояния «температура кипения – состав».

Под температурой кипения раствора понимают температуру, при которой общее давление насыщенного пара над раствором становится равным внешнему давлению. Если раствор идеальный, то при постоянном внешнем давлении P _вн = const справедливо:

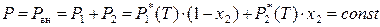. (8.28)

Для небольших температурных интервалов (согласно уравнению (5.20), глава 5) температурные зависимости давлений насыщенного пара чистых компонентов можно представить в виде следующих уравнений:

, .

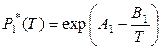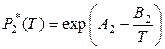Таким образом, во-первых, при постоянном внешнем давлении отсутствует линейная зависимость между составом раствора (х ₂) и температурой кипения раствора (T). Во-вторых, для расчета температуры кипения раствора необходимо знать свойства чистых компонентов – константы уравнения Клапейрона-Клаузиуса А ₁, А ₂, В ₁ и В ₂.

Тем не менее, диаграмму состояния идеального бинарного раствора «температура кипения – состав» можно построить для заданного внешнего давления, поскольку

,

,

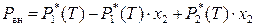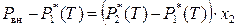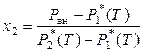, (8.29)

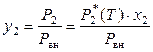. (8.30)

Зависимость температуры кипения идеального бинарного раствора от состава раствора и пара представлена на рис. 8.4.

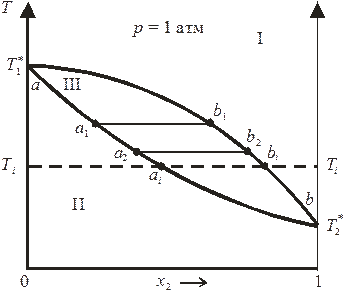
Рис. 8.4. Диаграмма состояния «температура кипения – состав»

идеального бинарного раствора.

В области I диаграммы существует только пар (газовый раствор), в области II — только жидкий раствор; область III является областью сосуществования пара и жидкого раствора. Нижняя кривая aa ₁ a ₂ …b называется кривой кипения; верхняя кривая ab ₁ b ₂ …b — кривой конденсаци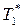и; и 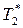— температуры кипения чистых жидкостей (компонентов).

Для случая, представленного на рис. 8.4, температура кипения второго компонента меньше температуры кипения первого компонента, поэтому второй компонент является более летучим (то есть при заданной температуре давление насыщенного пара второго чистого компонента выше по сравнению с первым компонентом). В области III состав жидкой и паровой фаз при любой температуре определяется пересечением изотермы T_i = const с кривыми кипения и конденсации (точки a_i и b_i для жидкого раствора и насыщенного пара соответственно), а соотношение между количествами фаз, сосуществующих в равновесии, подчиняется правилу рычага (рис. 8.5).

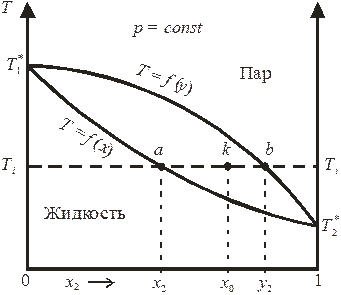
Рис. 8.5. Правило рычага в применении к диаграмме состояния

«температура кипения – раствор».

Дата добавления: 2014-01-04