
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Растворимость твердых веществ в жидкостях
|
|
|
|
Коллигативные свойства растворов.
Растворимость твердых веществ в жидкостях.
Под растворимостью обычно понимают способность вещества образовывать растворы с другими веществами. Растворимость твердого вещества в данном растворителе определяется концентрацией его насыщенного раствора при определенных температуре и давлении.
Насыщенный раствор – это раствор, находящийся в равновесии с кристаллами твердого вещества при заданных температуре и давлении. В насыщенном растворе химические потенциалы растворенного вещества в жидкой и твердой (кристаллической) фазах одинаковы:
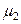 (р-р) =
(р-р) = 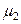 (кр) =
(кр) = 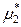 (кр). (9.1)
(кр). (9.1)
Если при растворении твердого вещества образуется идеальный раствор (идеальная растворимость твердых тел), то химический потенциал этого вещества в насыщенном растворе равен
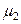 (р-р) =
(р-р) = 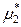 (ж) +
(ж) + 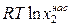 =
= 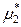 (кр), (9.2)
(кр), (9.2)
где 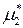 (ж) – химический потенциал чистого растворенного вещества в жидком состоянии.
(ж) – химический потенциал чистого растворенного вещества в жидком состоянии.
Тогда
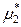 (ж) –
(ж) – 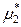 (кр) = –
(кр) = –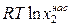 . (9.3)
. (9.3)
Левая часть уравнения (9.3) представляет собой разность химических потенциалов чистого вещества в жидком и твердом состоянии, равную изменению молярной энергии Гиббса при плавлении 1 моля растворенного вещества при температуре Т (температуре растворения) и давлении P:
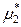 (ж) –
(ж) – 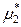 (кр) =
(кр) = 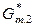 (ж) –
(ж) – 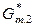 (кр) =
(кр) =  = –
= –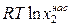 . (9.4)
. (9.4)
По уравнению Гиббса-Гельмгольца для процесса плавления растворенного вещества при постоянном давлении справедливо:
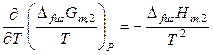 . (9.5)
. (9.5)
Тогда с учетом уравнения (9.4) получаем
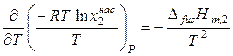 ,
,
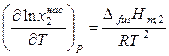 . (9.6)
. (9.6)
Уравнение (9.6) называют уравнением идеальной растворимости или уравнением Шредера. В нем отсутствуют величины, характеризующие индивидуальные свойства растворителя, поэтому идеальная растворимость твердых тел не зависит от природы растворителя.
Далее, поскольку энтальпия плавления растворенного вещества – величина всегда положительная, то
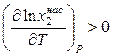 (9.7)
(9.7)
и идеальная растворимость твердых тел всегда увеличивается с ростом температуры.
Разделим переменные в уравнении (9.7) и проинтегрируем его в пределах от температуры плавления Tfus ,2 чистого растворенного вещества до температуры растворения T:
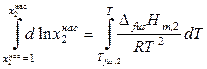 . (9.8)
. (9.8)
Если принять, что в интервале от Tfus ,2 до T энтальпия плавления растворенного вещества не зависит от температуры, то
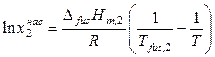 . (9.9)
. (9.9)
Мольная доля растворенного вещества в насыщенном растворе всегда меньше единицы, поэтому
 .
.
И действительно, энтальпия плавления вещества – величина положительная, а растворение твердых веществ ведут при температурах ниже их температур плавления, то есть
 ,
, 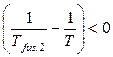 .
.
Мольная доля растворенного вещества в насыщенном растворе будет тем больше, чем больше будет величина правой части уравнения (9.9): например,
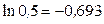 ;
;  .
.
Следовательно, чем больше температура плавления твердого вещества и чем больше его энтальпия плавления, тем меньше будет его идеальная растворимость.
Преобразуем уравнение (9.9):
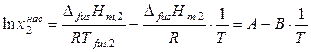 , (9.10)
, (9.10)
где коэффициенты А и В положительны. Таким образом, при образовании идеальных растворов логарифм растворимости твердого тела в жидкости, выраженной в мольных долях, линейно зависит от обратной величины абсолютной температуры.
Уравнение Шредера используется для оценки растворимости твердых органических веществ при оптимизации процессов их очистки методом перекристаллизации из растворов или для расчета необходимого количества растворителя для их полного растворения в заданных условиях.
Влияние давления на растворимость твердых тел в жидкостях менее существенно по сравнению с влиянием температуры и при постоянной температуре может быть оценено следующим образом:
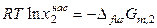 ,
,
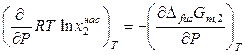 ,
,
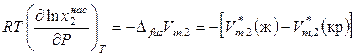 ,
,
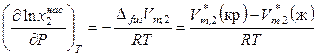 , (9.11)
, (9.11)
где 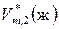 – молярный объем растворенного вещества в расплавленном (жидком) переохлажденном состоянии при температуре растворения;
– молярный объем растворенного вещества в расплавленном (жидком) переохлажденном состоянии при температуре растворения; 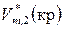 – молярный объем твердого растворенного вещества;
– молярный объем твердого растворенного вещества; 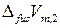 – изменение объема при плавлении 1 моля растворенного вещества при температуре растворения.
– изменение объема при плавлении 1 моля растворенного вещества при температуре растворения.
Выражение (9.11) называют уравнением Ван-Лаара. Поскольку для большинства веществ
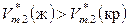 и
и 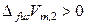 ,
,
то с увеличением давления при постоянной температуре идеальная растворимость твердых тел уменьшается.
Уравнение Шредера в форме (9.6) в большинстве случаев можно использовать и для неидеальных растворов, если заменить мольную долю на активность:
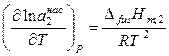 . (9.12)
. (9.12)
В этом случае за стандартное состояние растворенного вещества принимается чистая переохлажденная жидкость, а твердая фаза в насыщенном растворе должна состоять только из кристаллов растворенного вещества.
В термодинамике растворов важную роль играют теплоты или энтальпии растворения – изменения энтальпии при переходе жидкого, твердого или газообразного вещества в состояние раствора. Различают интегральные и дифференциальные теплоты растворения.
Интегральной теплотой или энтальпией растворения
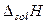
называют изменение энтальпии при растворении 1 моль вещества в некотором количестве чистого растворителя. Концентрацию раствора при этом обычно выражают величиной разбавления – числом молей растворителя в расчете на 1 моль растворенного вещества. Процесс растворения представляют термохимическим уравнением, например, процесс растворения a моль KNO3 в b моль воды можно записать в следующем виде:
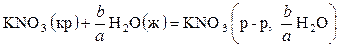 .
.
Интегральные теплоты растворения зависят не только от температуры, но и от концентрации полученного раствора, поэтому их число для данного сочетания растворитель – растворенное вещество может быть сколь угодно большим. Из всей этой совокупности величин выделяют первую и полную теплоты растворения. Первой интегральной энтальпией растворения называется изменение энтальпии при растворении 1 моль вещества в бесконечно большом количестве чистого растворителя (при этом образуется бесконечно разбавленный раствор). Например,
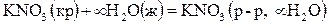 .
.
Полной интегральной энтальпией растворения называется изменение энтальпии при растворении 1 моль вещества в таком количестве чистого растворителя, которое необходимо для образования насыщенного раствора (при данной температуре).
Дифференциальной (или парциальной) теплотой растворения
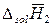
называется изменение энтальпии при растворении 1 моль вещества в бесконечно большом количестве раствора заданной концентрации. При этом концентрация раствора остается неизменной или, точнее, возрастает на бесконечно малую величину, которой можно пренебречь. Дифференциальная теплота растворения зависит от температуры и концентрации.
Дифференциальная теплота растворения 1 моль вещества в бесконечно большом количестве бесконечно разбавленного раствора совпадает с первой интегральной теплотой растворения. Дифференциальная теплота растворения 1 моль вещества в бесконечно большом количестве насыщенного раствора называется последней теплотой растворения.
На практике именно величину последней теплоты растворения используют для характеристики растворимости твердых веществ в жидкостях при образовании реальных растворов, при этом уравнение растворимости принимает вид
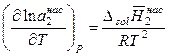 . (9.13)
. (9.13)
Величина последней теплоты растворения зависит не только от природы растворяемого вещества, но и от природы растворителя и присутствия в растворе посторонних веществ, поэтому она может быть как больше, так и меньше нуля. Значит, неидеальная растворимость твердых веществ может как увеличиваться, так и уменьшаться с ростом температуры.
Следует отметить, что сам процесс растворения 1 моль твердого вещества в бесконечно большом количестве насыщенного раствора можно представить в виде суммы двух процессов: плавления 1 моль твердого вещества и смешения полученной жидкости с исходным жидким раствором, то есть
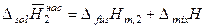 . (9.14)
. (9.14)
При образовании идеального раствора энтальпия смешения равна нулю и
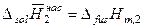 ,
,
активность растворенного вещества равна его мольной доле
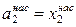 ,
,
поэтому уравнение (9.13) преобразуется в уравнение Шредера вида (9.6).
Разделим переменные в уравнении (9.13) и затем проинтегрируем полученное выражение в пределах от T 1 до Т 2, в результате получим
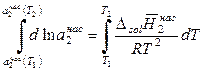 ,
,
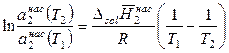 . (9.15)
. (9.15)
Левая часть уравнения (9.15) представляет собой логарифм отношения растворимостей вещества при двух температурах. Насыщенные растворы труднорастворимых солей являются очень разбавленными и для них отношение активностей в первом приближении можно заменить отношением концентраций, тогда
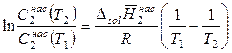 .
.
Зная температурную зависимость концентрации насыщенного раствора труднорастворимой соли, можно определить ее последнюю (дифференциальную) теплоту растворения.
В заключение следует отметить, что растворы заданной концентрации можно получить, растворяя жидкие, твердые или газообразные вещества в растворителе или разбавляя концентрированный раствор. Тепловой эффект взаимодействия раствора данной концентрации с чистым растворителем называется энтальпией разбавления (разведения) и обозначается символом
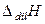 .
.
Если раствор, содержащий 1 моль растворенного вещества, разбавляется от данной исходной до бесконечно малой концентрации (с образованием бесконечно разбавленного раствора), то энтальпия разбавления называется интегральной. Если к бесконечно большому количеству раствора добавляется 1 моль чистого растворителя, то тепловой эффект процесса называется дифференциальной теплотой разбавления.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 7560; Нарушение авторских прав?; Мы поможем в написании вашей работы!