
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понижение температуры замерзания растворов. Криоскопия
|
|
|
|
КОЛЛИГАТИВНЫЕ СВОЙСТВА РАСТВОРОВ
Физические и химические свойства растворов разнообразны. Они отличаются по цвету, удельному весу, удельной электропроводности, показателю преломления, температуре кипения и замерзания. В отдельную группу из всего многообразия свойств растворов выделяют такие свойства, которые прямо пропорционально зависят от концентрации растворенного вещества, точнее, от количества частиц растворенного вещества, но нет от его природы. Эти свойства растворов называют коллигативными (зависящими от числа молекул). Обычно выделяют четыре коллигативные свойства растворов: понижение давления пара растворителя, понижение температуры замерзания, повышение точки кипения и осмотическое давление. Основным коллигативным свойством раствора является понижение давления пара растворителя над раствором, а остальные являются следствием из него.
При изучении коллигативных свойств растворов обычно принимают два ограничения. Во-первых, растворенное вещество является нелетучим и, следовательно, в паре присутствует только растворитель. Во-вторых, растворенное вещество не образует с растворителем твердых растворов (не растворимо в твердом растворителе). С термодинамической точки зрения уменьшение давления насыщенного пара растворителя над раствором обусловлено уменьшением химического потенциала растворителя в присутствии растворенного вещества (иначе раствор не образовывался бы). Уменьшение химического потенциала растворителя приводит к понижению температуры замерзания и повышению температуры кипения растворов, а также возникновению осмотического давления. Найдем количественную связь между указанными свойствами.
Жидкость начинает замерзать, когда химические потенциалы компонента в жидкой и твердой фазах становятся одинаковыми. Поэтому под температурой замерзания раствора понимается температура, при которой устанавливается равновесие между кристаллами растворителя и раствором, фактически при этой температуре раствор становится насыщенным относительно растворителя. Из равенства химических потенциалов растворителя в твердой фазе и жидком растворе в точке замерзания следует, что при температуре замерзания давление пара растворителя над раствором и над кристаллами одинаково.
Итак, если твердая фаза представлена только кристаллами чистого растворителя, то при температуре замерзания раствора
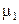 (р-р) =
(р-р) = 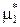 (кр). (9.16)
(кр). (9.16)
Если к тому же раствор достаточно разбавлен или идеален, то парциальное давление пара растворителя подчиняется закону Рауля и
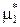 (кр) =
(кр) = 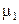 (р-р) =
(р-р) = 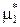 (ж) +
(ж) + 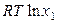 . (9.17)
. (9.17)
Произведем преобразования уравнения (9.17), аналогичные представленным в п. 9.1 при выводе уравнения идеальной растворимости твердых тел, в результате получим:
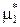 (ж) –
(ж) – 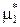 (кр) = –
(кр) = –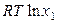 ,
,
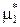 (ж) –
(ж) – 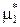 (кр) =
(кр) =  (ж) –
(ж) – 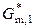 (кр) =
(кр) =  = –
= –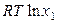 ,
,
 ,
, 
 , (9.18)
, (9.18)
 ,
,
 , (9.19)
, (9.19)
где 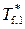 и
и  – температуры замерзания чистого растворителя и раствора соответственно (нижний индекс f от англ. «freezing»).
– температуры замерзания чистого растворителя и раствора соответственно (нижний индекс f от англ. «freezing»).
Поскольку для растворов  , а
, а 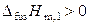 , то
, то
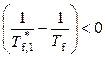 и
и  .
.
Температура замерзания чистого растворителя всегда выше, чем температура замерзания раствора. При этом в рамках принятых допущений температура замерзания раствора зависит от его концентрации (мольной доли растворителя) и от свойств растворителя (температуры замерзания и энтальпии плавления).
Для бинарных растворов уравнение (9.19) можно записать в следующем виде:
 ,
,
 , (9.20)
, (9.20)
где Δ T f – понижение температуры замерзания раствора. В разбавленных растворах x 1 >> x 2, x 2 и Δ T f – малые величины, поэтому
 ,
, 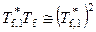 ,
,
и уравнение (9.20) принимает вид
 . (9.21)
. (9.21)
В разбавленных растворах мольная доля растворенного вещества и его моляльность (m 2, моль∙кг–1) связаны соотношением
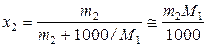 ,
,
где M 1 – молярная масса растворителя. Поэтому
 , (9.22)
, (9.22)
где
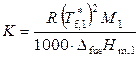 .
.
Величину К называют криоскопической постоянной растворителя или моляльным понижением температуры замерзания раствора (если m 2 = 1, то Δ T f = К). Например, криоскопическая постоянная воды равна 1.86, бензола – 5.12, циклогексана – 20.0.
В случае бинарного раствора по уравнению (9.22) можно определить молярную массу растворенного вещества М 2. Обозначим через g 1 и g 2 массы (г) растворителя и растворенного вещества. Тогда g 2/ M 2 молей растворенного вещества содержатся в g 1 г растворителя; а m 2 молей растворенного вещества содержатся в 1000 граммах растворителя. Следовательно,
 ,
, 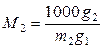 .
.
Поскольку
 ,
,
то
 . (9.23)
. (9.23)
Метод определения молярной массы растворенного вещества, основанный на явлении понижения температуры замерзания раствора по сравнению с чистым растворителем, называется криоскопическим или просто криоскопией. Надежные результаты по этому методу получаются, если, во-первых, при растворении исследуемого вещества не происходит диссоциация или ассоциация его молекул и, во-вторых, используются растворители с высокими значениями криоскопических постоянных.
В растворах электролитов диссоциация растворенного вещества приводит к увеличению числа частиц в растворе по сравнению с их исходным количеством, поэтому уравнение (9.22) принимает вид
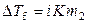 , (9.24)
, (9.24)
где i – изотонический коэффициент Вант-Гоффа, показывающий, во сколько раз увеличилось число частиц в растворе вследствие диссоциации. Уравнение (9.24) позволяет определить экспериментальное значение изотонического коэффициента раствора электролита известной моляльности на основе опытной величины понижения его температуры замерзания. Теоретическое значение изотонического коэффициента Вант-Гоффа может быть рассчитано по формуле:
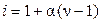 , (9.25)
, (9.25)
где α – степень диссоциации; ν – число ионов, на которые распадается исходная частица. Отличия опытных значений изотонического коэффициента от теоретических обусловлены электростатическим взаимодействием ионов в растворах электролитов. Так, например, для растворов сильных электролитов α = 1 и согласно уравнению (9.25) i должен быть равен ν, а на практике i всегда меньше ν.
Уравнения (9.18) и (9.19), справедливые для предельно разбавленных и идеальных растворов, могут быть формально использованы и для реальных растворов при замене мольной доли растворителя на его активность. Соответствующие уравнения имеют вид
 , (9.26)
, (9.26)
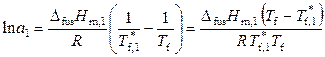 , (9.27)
, (9.27)
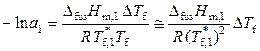 . (9.28)
. (9.28)
Уравнения (9.27) и (9.28) могут быть использованы для определения активности растворителя.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1849; Нарушение авторских прав?; Мы поможем в написании вашей работы!