П Л А Н. 1. Метод безпосереднього інтегрування

Завдання додому

Конспект; [1] с. 336 – 342

[2] с. 256 - 266

Питання для самоконтролю

1. Метод безпосереднього інтегрування.

2. Метод підстановки (заміни змінної).

3. Метод інтегрування частинами.

Л Е К Ц І Я 21

Тема: Інтегрування раціональних дробів.

Мета: ознайомити з розкладанням правильного дробу на суму найпростіших, нтегруванням раціонального дробу, інтегруванням виразів, які містять квадратний тричлен.

Література: [1, с. 352-355]; [6, с. 358-364].

1. Розкладання правильного дробу на суму найпростіших.

2. Інтегрування раціонального дробу.

3. Інтегрування виразів, які містять квадратний тричлен.

1. Означення. Відношення двох многочленів називається раціональним дробом.

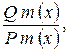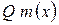де і 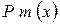- многочлени степеня m і n відповідно.

Якщо m<n, то дріб називається правильним.

Якщо m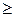n, то дріб називається неправильним.

Приклад: 1) 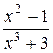- правильний дріб.

2) 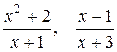- неправильні дроби.

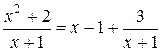
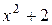
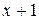
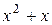
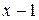
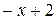
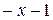
Щоб знайти інтеграл від неправильного раціонального дробу, потрібно виділити цілу частину шляхом ділення чисельника на знаменник:

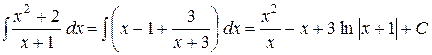
Щоб знайти інтеграл від правильного раціонального дробу, потрібно розкласти його на суму елементарних дробів.

Є чотири види елементарних правильних раціональних дробів.

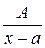І ІІ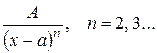

ІІІ 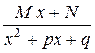IV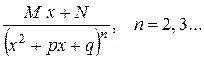

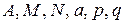- дійсні числа, а тричлен 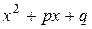не має дійсних коренів, тобто .

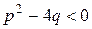Якщо знаменник правильного раціонального дробу розкладено на множники (а всякий многочлен з дійсними коефіцієнтами можна розкласти на лінійні та квадратні (з комплексними коренями) множники з дійсними коефіцієнтами), то такий дріб можна подати у вигляді суми простіших (елементарних) дробів, чисельники яких невідомі.

Якщо в розкладі знаменника на множники є множник 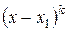, де

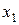- дійсний корінь, то елементарних дробів буде k такого виду:

, ,..., .

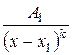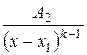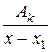Якщо в розкладі знаменника є множник виду (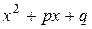)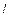, то елементарних дробів буде l такого виду:

, ,...,

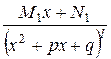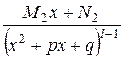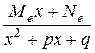
Числа А₁, А₂,..., А_k, М₁, N₁, M₂, N₂, …, M_e, N_e потрібно знайти.

Знаходять ці числа (чисельники) одним із методів: 1) порівнювання коефіцієнтів; 2) окремих значень аргументу або комбінують ці два методи.

Приклад: Правильний елементарний дріб розкласти на суму елементарних дробів:

++++

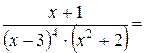
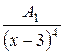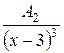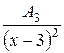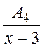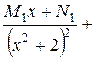
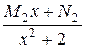
1) Метод порівнювання коефіцієнтів (або метод невизначених коефіцієнтів).

Суму елементарних дробів зводять до спільного знаменника.

Прирівнюють чисельники дробів лівої і правої частини рівності.

З попередньої тотожності складемо систему лінійних рівнянь при однакових степенях х; з цієї системи знайдемо невідомі чисельники елементарних дробів.

Приклад: Розкласти дріб на суму елементарних дробів.

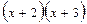
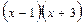
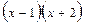
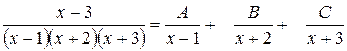
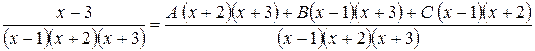
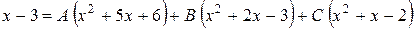
Прирівняємо коефіцієнти при однакових степенях х, починаючи з х в старшому степені:

х² 0=А+В+С

х 1=5А+2В+С

вільні члени – 3=6А – 3В – 2С

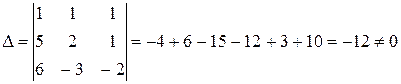
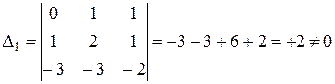
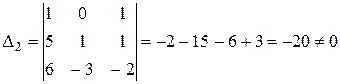
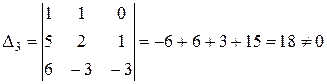
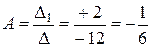
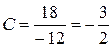
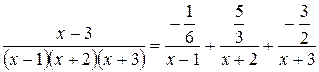
2) Метод окремих значень аргументу.

Якщо корені знаменника дійсні і прості, то для обчислення А, В, С можна застосувати метод підстановки коренів знаменника.

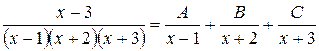
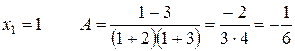
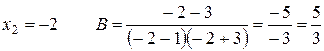
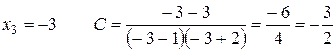
2,3. Інтеграли від елементарних дробів.

І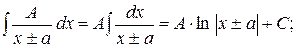

ІІ

ІІІ =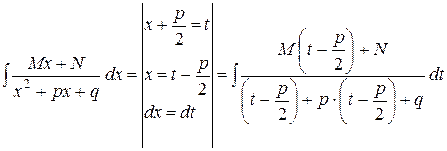

=

=

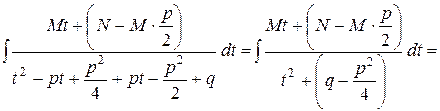
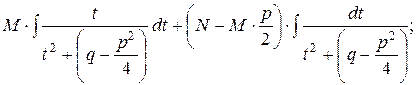
Перший інтеграл буде дорівнювати

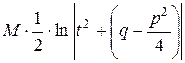
Другий інтеграл – табличний.

IV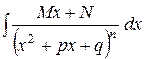

Підстановкою 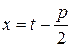зводиться до двох інтегралів:

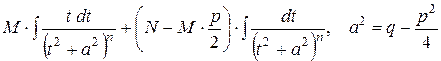
Перший інтеграл обчислюється безпосередньо.

Другий - за рекурентною формулою.

Дата добавления: 2014-01-04