Окружность, как частный случай эллипса

Уравнение (33.4) было получено в предположении, что F₁ и F₂ ––различные точки, то есть c > 0. Тогда b < a. Но кривую, определяемую уравнением (33.4), мы можем рассмотреть и в случае a = b, c = 0. Уравнение (33.4) в этом случае после умножения на a² примет вид x² + y² = a². Это –– уравнение окружности радиуса a с центром в начале координат. Таким образом, можно рассматривать окружность как частный эллипса, когда b=a и c=0 или, как иногда говорят математики, окружность является "вырожденным" эллипсом, у которого фокусы совпали.

Эксцентриситет 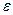эллипса характеризует степень вытянутости эллипса. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 0 < 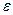< 1, ибо , а .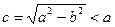

Если задано каноническое уравнение эллипса и требуется его построить, то для отображения качественных характеристик достаточно правильно отметить вершины эллипса и провести через них линию, похожую на кривую рис. 33.3, выдерживая симметрию и избегая образования углов на рисунке. Если же из рисунка предполагается получать числовую информацию о координатах его точек, то тогда построение следует проводить более точно. Нужно построить по точкам верхнюю половину эллипса, как график функции взяв для построения достаточно много точек, а нижнюю половину эллипса получить, используя его симметрию.

Дата добавления: 2014-01-04