Гипербола

Их эксцентриситет, фокусы и директрисы. Асимптоты гиперболы.

Гипербола и парабола как кривые второго порядка.

Известно, что кривая, задаваемая уравнением 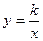, где k –– какое-то число, называется гиперболой. Однако это –– частный случай гиперболы (равносторонняя гипербола).

Определение 34.1 Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная. Для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось Ox направим вдоль этого отрезка, а ось ординат –– перпендикулярно к нему.

Теорема 34.1. Пусть расстояние между фокусами F₁ и F₂ гиперболы равно 2c, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a. Тогда гипербола в выбранной выше системе координат имеет уравнение

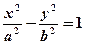
(34.1)

где

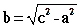
(34.2)

Доказательство. Пусть M(x; y) –– текущая точка гиперболы (рис. 1).

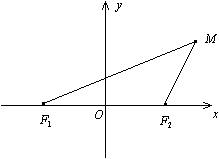
Рис. 34.1

Так как разность двух сторон треугольника меньше третьей стороны, то

|F₁M – F₂M| < F₁F₂, то есть 2a < 2c, a < c. В силу последнего неравенства вещественное число b, определяемое формулой (34.2), существует.

По условию, фокусы –– F₁ (-c; 0), F₂ (c; 0). Легко заметить, что

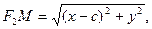
По определению гиперболы

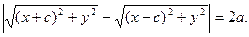
Это уравнение запишем в виде

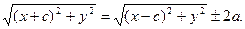
Обе части возведем в квадрат:

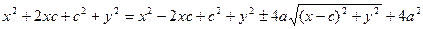
После приведения подобных членов и деления на 4, приходим к равенству

Опять обе части возведем в квадрат:

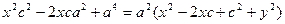
Раскрывая скобку и приводя подобные члены, получим

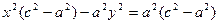
С учетом формулы (34.2) уравнение принимает вид

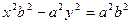
Разделим обе части уравнения на 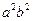и получим уравнение (34.1)

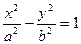
Определение 34.2 Уравнение (34.1) называется каноническим уравнением гиперболы.

Свойство 34.1. Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси Ox и Oy, а начало координат –– центр симметрии гиперболы.

Доказательство. Проводится аналогично доказательству свойства 1 для эллипса.

Проведем построение гиперболы, заданной уравнением (34.1). Заметим, что из-за симметрии достаточно построить кривую только в первом координатном угле. Выразим из канонического уравнения y как функцию x, при условии, что y > 0,

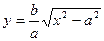
и построим график этой функции.

Область определения –– полупрямая [a; +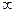), y(a)=0. Функция монотонно растет. Производная

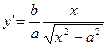
существует во всей области определения, кроме точки a. Следовательно, график –– гладкая кривая (без углов). Вторая производная

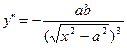
во всех точках интервала (a; +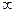), отрицательна, следовательно, график -- выпуклый вверх.

Проверим график на наличие асимптоты при . Пусть асимптота имеет уравнение 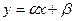. Тогда по правилам математического анализа

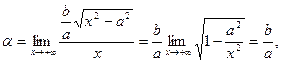
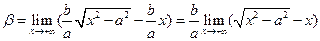
Выражение под знаком предела домножим и разделим на 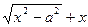. Получим

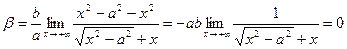
Итак, график функции имеет асимптоту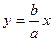. Из симметрии гиперболы следует, что 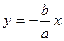–– тоже асимптота. Остается неясным характер кривой в окрестности точки (x=a), а именно, образует ли график 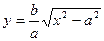и симметричная ему относительно оси Ox часть гиперболы в этой точке угол или гипербола в этой точке –– гладкая кривая (есть касательная). Для решения этого вопроса выразим из уравнения (34.1) x через y:

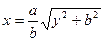
Очевидно, что данная функция имеет производную в точке y=0, x’(0)=0, и в точке (a; 0) у гиперболы есть вертикальная касательная. По полученным данным рисуем график функции 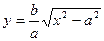(рис. 34.2).

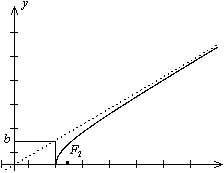
Рис. 34.2.График функции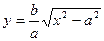

Окончательно, используя симметрию гиперболы, получаем кривую рисунка 34.3.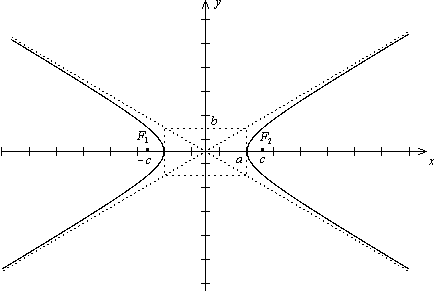

Рис. 34.3. Гипербола

Определение 34.3. Точки пересечения гиперболы, заданной каноническим уравнением (34.1), с осью Ox называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками (0; -b) и (0; b) называется мнимой осью. Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина 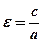называется эксцентриситетом гиперболы.

Прямые и 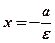называются директрисами гиперболы, а прямые 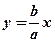и 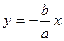- ее асимптотами (ранее было показано, что эти прямые будут асимптотами и согласно определениям математического анализа). Прямоугольник, диагоналями которого являются асимптоты гиперболы, а пара его параллельных сторон проходят через ее вершины, называется основным прямоугольником гиперболы (Тогда оси гиперболы параллельны сторонам ее основного прямоугольника).

Из равенства (34.2) следует, что c > a, то есть у гиперболы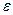>1. Эксцентриситет 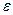характеризует угол между асимптотами (в котором лежит гипербола), чем ближе 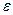к 1, тем меньше этот угол.

В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинам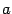и и 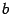может быть произвольным. В частности, при 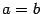мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид 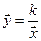, если взять k=0.5a², а ос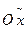и и 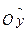направить по биссектрисам четвертого и первого координатных углов (рис. 33.4). В самом деле уравнение 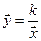при 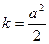легко сводится к виду 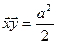. Положив далее 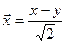, а 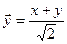(что соответствует повороту осей на угол π/4(смотри напр. §35, формула (35.4)), из уравнения 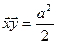получим 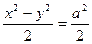. Поделив последнее равенство на 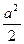, получим уравнение (34.1) при b=a.

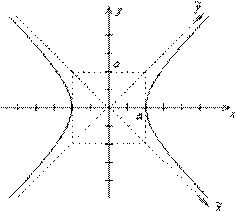
Рис. 33.4.Равносторонняя гипербола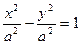

Для отражения на рисунке качественных характеристик гиперболы достаточно определить ее вершины, нарисовать асимптоты и нарисовать гладкую кривую, проходящую через вершины, приближающуюся к асимптотам и похожую на кривую рисунка 34.2.

Дата добавления: 2014-01-04