Двуполостной гиперболоид

Определение 47.3. Двуполостным гиперболоидом называется поверхность, координаты всех точек которой в некоторой системе координат удовлетворяют уравнению

(47.20)

Общий вид двуполостного гиперболоида изображён на рис.47.7

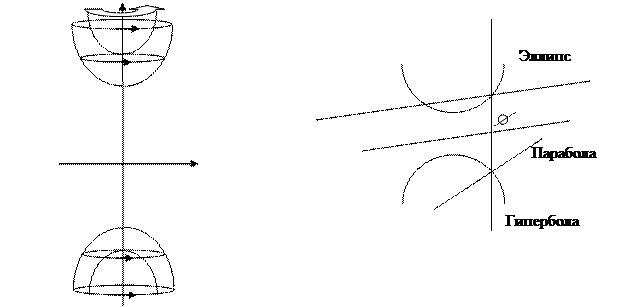
Рис.47.8 Рис.47.9

При вращении гиперболы вокруг пересекающей её оси симметрии получится двуполостной гиперболоид вращения. (см. рис. 47.8)

В сечении двуполостного гиперболоида плоскостями могут получаться (см.рис 47.9, на котором гиперболоид и все секущие его плоскости изображены «сбоку»);

- эллипс (из рис.47.9 видно, что в сечении двуполостного гиперболоида плоскостью эллипс должна получиться некоторая ограниченная кривая второго порядка, т.е. эллипс);

- гипербола (согласно рис. 47.9, в сечении двуполостного гиперболоида плоскостью гипербола получается разрывная кривая второго порядка, т.е гипербола);

- парабола (получается в сечении двуполостного гиперболоида плоскостью, параллельной образующей его асимптотического конуса; читателю предлагаем самостоятельно из рис. 47.9 установить, что тогда в сечении возникает некоторая неограниченная непрерывная кривая второго порядка, т.е. парабола)

-одна точка (если секущая плоскость касается двуполостного гиперболоида);

-пустое множество (когда плоскость двуполостный гиперболоид не пересекает).

Остальные линии второго порядка в сечении двуполостного гиперболоида плоскостью получить нельзя.

В отличие от эллипсоидов, все виды которого можно перевести друг в друга (и, в том числе, и в сферу) с помощью некоторого линейного преобразования (например, непропорциального сжатия осей), однополостный и двуполостный гиперболоиды – совсем разные поверхности, которые нельзя перевести друг в друга никаким линейным преобразованием координат. Это, например, следует из того, что в сечении однополостного гиперболоида некоторой плоскостью можно получить две пересекающихся прямых линии, что нельзя сделать для двуполостного гиперболоида.

Более того, однополостный гиперболоид – связная (точнее, даже линейно связная) поверхность (т.е всякие две его точки можно соединить непрерывной линией, целиком лежащей на данной поверхности), а двуполостный гиперболоид связной поверхностью не являются.

Дата добавления: 2014-01-04