Правило 2

Це правило допомагає запам'ятати співвідношення

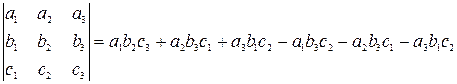
за допомогою такого рисунка:

На рисунку лініями з'єднані коефіцієнти, що входять у відповідні добутки, а знаки плюс і мінус указують на знак, з яким цей добуток входить у визначник.

Правило 3. Використання додаткових стовпців.

Відповідно до цього правила достатньо праворуч від визначника дописати перший, а потім другий стовпець. Потім у визначник включають зі знаком плюс добуток коефіцієнтів, що стоять по головній діагоналі і паралельній їй діагоналях, а зі знаком мінус – коефіцієнти, що стоять по малій діагоналі й паралельній їй діагоналях.

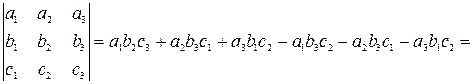
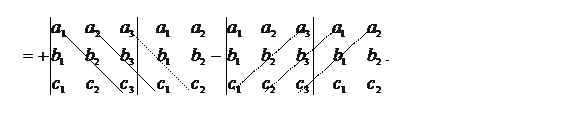
Відомості про векторний добуток.

2.11. Визначення змішаного добутку.

.

____________________________________________________________________

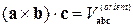8.2. Властивості змішаного добутку.

Змішаний добуток компланарних векторів дорівнює нулю:

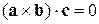
Змішаний добуток, що містить два однакових вектори, дорівнює нулю.

Другу властивість ми одержимо, якщо спробуємо обчислити змішаний добуток, у якому вектори переставимо циклічно: 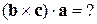. Результатом такого добутку буде об’єм того ж орієнтованого паралелепіпеда:

,

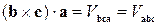а, отже, циклічні перестановки співмножників у мішаному добутку не змінюють його.

Отже, звичайні перестановки змінюють знак змішаного добутку 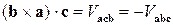. Ці два правила можна представити таким ланцюжком рівностей:

.

.

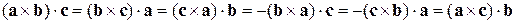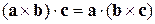Це властивість можна виразити у вигляді такого правила: у змішаному добутку знаки множення можна змінювати місцями.

.

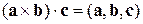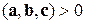
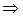
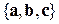– права трійка векторів;

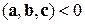
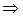
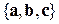– ліва трійка векторів.

Розподільний закон змішаного добутку можна довести, хоча б для одного з векторів у добутку, наприклад, для вектора, що стоїть на останньому місці:

.

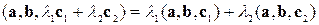Щоб довести цю рівність, достатньо представити змішаний добуток 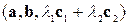у його початковому вигляді:

,

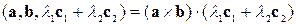а потім скористатися дистрибутивністю скалярного добутку, що дозволяє нам розкривати дужки: .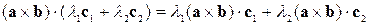

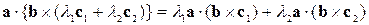
– розподільний закон векторного добутку векторів.

Звідси отримуємо також вираз для розподільного закону векторного добутку векторів:

.

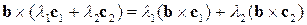8.3. Змішаний добуток у декартовому базисі.

.

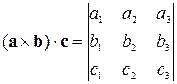8.4. Приклади застосування змішаного добутку під час розв’язування задач.

Задача 8.1. Представити заданий вектор 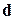у вигляді розкладання довільного вектора по трьох заданих некомпланарних векторах 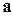, 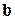і .

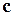За умовою задачі необхідно представити вектор 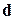у такому вигляді:

. (8.1.1)

Шукані коефіцієнти 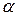, 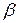і являють собою не що інше, як координати вектора 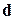у базисі, складеному з векторів 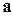, 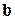і 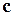. Існування й одиничність такого представлення ми досліджували в розділах 3, 4.

Щоб розв’язати задачу скористаємося тією властивістю змішаного добутку, відповідно до якої мішаний добуток, що містить два однакових вектори дорівнює нулю. Помножимо співвідношення (8.1.1) ліворуч і праворуч на векторний добуток :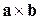

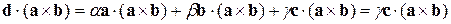. (8.1.2)

Звідси можна знайти коефіцієнт

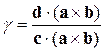. (8.1.3)

Помітимо, що відповідно до умови задачі величина 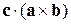, що стоїть у чисельнику, не дорівнює нулю. Отриманий результат можна переписати іншим образом:

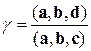. (.8.1.4)

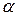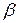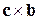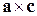Аналогічно одержуємо коефіцієнти і множачи співвідношення (8.1.1) на величини і , відповідно:

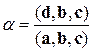
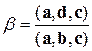. (8.1.5)

Отримані результати можна запам'ятати за допомогою такого простого правила. Коефіцієнт у розкладанні вектора по базису дорівнює дробу, в знаменнику якого стоїть мішаний добуток базисних векторів, а в чисельнику – цей же мішаний добуток, у якому даний вектор стоїть замість базисного вектора, що відповідає шуканій координаті.

Задача 8.2. Визначте вектор 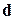по заданих скалярних добутках 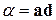, 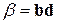і .

1. Прийом, що ми застосували в першій задачі, може допомогти нам і тут. Але для цього необхідно придумати таке розкладання вектора 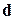, щоб після відповідних скалярних множень вийшли найбільш прості вирази, що бажано містять по одному з невідомих коефіцієнтів розкладання. Одне з таких розкладань має вигляд:

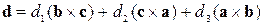. (8.2.1)

Справді, після скалярного множення на кожний з векторів 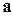, 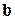і 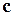праворуч буде залишатися тільки один з доданків. У той же час ліворуч будуть виходити задані за умовою задачі відповідні скалярні добутки. Наприклад:

. (8.2.2)

Звідси одержуємо:

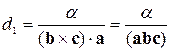. (8.2.3)

Аналогічно і для інших коефіцієнтів:

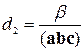та 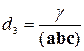. (8.2.4)

У підсумку для вектора 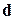одержуємо остаточний вираз:

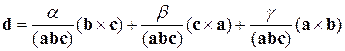. (8.2.5)

Ми бачимо, що для існування розв’язку необхідно, щоб принаймні знаменники в (8.2.5) не дорівнювали нулю, тобто вектори 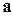, 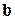і 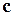не були компланарними.

2. Однак, для того щоб такий розв’язок був можливим, нам необхідно переконатися в існуванні розкладання (8.2.1), тобто треба довести, що вектори 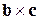, 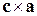і 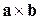можна обрати як базис. Для цього необхідно переконатися в їх некомпланарності, тобто визначити, коли їхній мішаний добуток не дорівнює нулю:

. (8.2.5)

У наступному розділі ми доведемо, що цей вираз зводиться до мішаного добутку 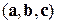і, тим самим, ми знову, як умову існування розв’язку цієї задачі, одержуємо, що вектори повинні бути некомпланарними.

8.4. Подвійний векторний добуток векторів.

8.5. Задачі

Задача 8.3. (продовження задачі 5.1). Знайдіть компонент вектора 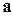, ортогональний векторові .

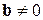Розв’язок. У задачі 5.1. був знайдений компонент 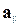вектора 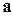, паралельний ненульовому векторові :

.

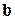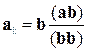Звідси можна знайти компонент вектора 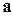, перпендикулярний векторові :

.

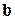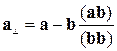Тепер приведемо праву частину цього виразу до загального знаменника:

.

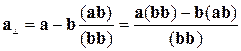У чисельнику стоїть не що інше, як подвійний векторний добуток 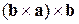. Отже, шуканий вираз для виглядає так:

.

Задача 8.4. (закінчення задачі 8.2)

Спростити вираз .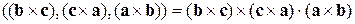

Розв’язок. Щоб розв’язати задачу розглянемо подвійний векторний добуток 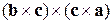, де як перший вектор візьмемо 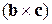, другий – 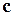, а третій – 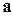. Тоді

.

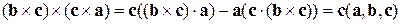Множачи цей добуток на 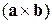, одержуємо

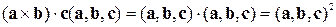
Таким чином, ми показали, що некомпланарність векторів 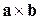, 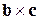і 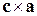еквівалентна некопланарності векторів 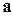, 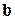і 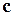, тобто

.

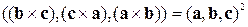Задача 8.5. Довести, що

.

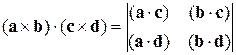Розв’язок. Величина 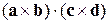являє собою мішаний добуток трьох векторів 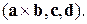Отже, у ньому можна переставити знаки місцями:

.

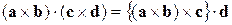У фігурних дужках стоїть подвійний векторний добуток, що розкриваємо відповідно до правила:

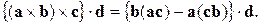
Розкриваючи фігурні дужки, остаточно одержуємо шукане співвідношення.

.

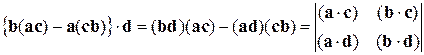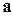Відзначимо окремий випадок співвідношення , у якому вектори і 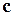, а також 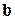і 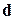збігаються:

.

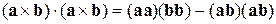Це співвідношення зв'язує довжини векторного й скалярного добутку двох векторів:

.

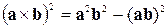Причому останнє співвідношення можна довести прямо з визначень довжин векторного і скалярного добутку:

.

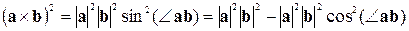Ця рівність справедлива через співвідношення .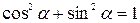

Задача 8.6. Доведіть, що

.

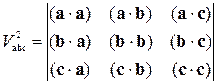Дата добавления: 2014-01-04