Изучение процессов сложения колебаний с помощью электронного осциллографа

Лабораторная работа №4

Внимание!

После каждых 30 минут непрерывной работы аппарата делайте не менее чем 10-минутный перерыв. Если дальнейшее проведение эксперимента не предвидится, произведите полное отключение аппарата. Для этого выключатель СЕТЬ переведите в положение ВЫКЛ, при этом должен погаснуть индикатор сети, выньте вилку сетевого шнура из розетки.

Контрольные вопросы

1. Что такое магнитотерапия? 2. Какие процессы имеют место при магнитотерапии? 3. Какой параметр магнитного поля используется в магнитотерапии? 4. Что такое магнитная индукция? Магнитный поток? 5. Для каких целей используют аппарат «Полюс – 2»? 6. В каких режимах и на каких частотах может работать аппарат «Полюс – 2»?

Приборы и принадлежности: два звуковых генератора ГЗ-33, электронный осциллограф ОДШ-2, соединительные провода.

Цель работы: изучение результата сложения гармонических колебаний, происходящих в одном направлении, и взаимно перпендикулярных колебаний.

Колебания представляют собой один из наиболее распространенных видов движения.

Движение, при котором по истечении определенного промежутка времени, периода колебания, точка возвращается в то же самое состояние движения, т.е. занимает то же положение и имеет ту же скорость, ускорение, называется периодическим.

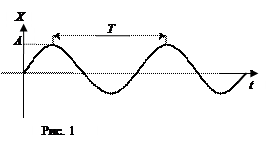На рис. 1 показан график периодически изменяющейся величины Х как функции времени t. Кроме периода Т, периодическое (колебательное) движение характеризуется наибольшим отклонением А колеблющейся точки от положения равновесия (Х=0), которое называется амплитудой колебания.

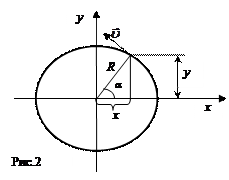
Среди периодических колебаний существенную роль играют так называемые гармонические колебания. Гармонические колебания представляют собой периодический процесс, в котором изменение величины происходит по закону синуса или косинуса. Гармонические колебания можно рассматривать как проекцию точки, движущейся по окружности, на линию, лежащую в плоскости движения точки (рис. 2). Если окружность имеет радиус R, а угловая скорость вращения точки w, то

, (1)

где wt – фаза колебания.

По истечении одного или нескольких интервалов времени Т, соответствующих периоду колебания, движущаяся точка должна занять свое прежнее положение. Следовательно, период колебания Т определяется из условия:

(2)

Так как косинус имеет период 2p, то на основании уравнения (2) ясно, что период гармонического колебания будет выражаться формулой:

,

где 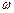– круговая или циклическая частота гармонических колебаний.

Величина, обратная периоду колебаний, называется частотой колебаний:

.

Если одна и та же частица участвует в нескольких колебательных движениях одновременно, то смещение точки в каждый момент времени можно найти геометрически, векторно сложив ее смещения от каждого колебания в отдельности. Рассмотрим два частных случая сложения колебаний.

Дата добавления: 2014-01-04