Изучение затухающих механических колебаний с помощью электрического кимографа

Лабораторная работа № 5

Приборы и принадлежности: электрический кимограф, колебательное устройство - пружинный маятник, укрепленный на штативе, писчик, секундомер, линейка, клей, бумага, калькулятор.

Цель работы: изучение затухающих механических колебаний и ознакомление с простейшим самописцем — электрическим кимографом.

Колебания - движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания свойственны многим явлениям природы: пульсирует излучение звезд, внутри которых происходят циклические ядерные реакции; с высокой степенью периодичности вращаются планеты Солнечной системы; движение Луны вызывает отливы и приливы на Земле; в земной ионосфере и атмосфере циркулируют потоки заряженных и нейтральных частиц; ветры возбуждают колебания и волны на поверхности водоемов и т.д.

В физике выделяют колебания механические, электромагнитные и их комбинации. Это обусловлено той исключительной ролью, которую играют гравитационные и электромагнитные взаимодействия в масштабах, характерных для жизнедеятельности человека. С помощью распространяющихся механических колебаний плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых колебаний электрических и магнитных полей, воспринимаемых нами как свет, мы получаем большое число прямой информации об окружающем мире.

В технике колебания либо выполняют определенные функциональные обязанности (маятник, колебательный контур, генератор колебаний и др.), либо возникают как неизбежное проявление физических свойств (вибрации машин и сооружений, неустойчивости и вихревые потоки при движении тел в газах и др.).

В виде сложнейшей совокупности колебаний частиц (электронов, фотонов, протонов и др.) и полей можно представить “устройство” микромира.

Внутри любого организма непрерывно происходят разнообразные, ритмично повторяющиеся процессы.

Организм человека является сложной динамической системой. Трудно указать физиологический процесс, протекающий в организме, который бы не изменялся во времени. Как правило, эти процессы подвержены ритмическим изменениям — это и колебания вокруг равновесного состояния (например, изменение концентрации химически активных веществ), и целенаправленные изменения частоты и формы сигналов (например, электрическая активность нервных клеток), и механические колебания, связанные с механической активностью органов. С удивительной надежностью бьется человеческое сердце, даже психика людей подвержена колебаниям. Сигналы, характеризующие эти изменения, разнообразны по своей природе, форме, частоте, интенсивности. Очень широк диапазон частот сигналов, которые можно получить от живого организма, — от долей Герца до 10¹⁴ Гц.

Несмотря на разную природу колебаний, в них обнаруживаются одни и те же физические закономерности: они описываются одними и теми же уравнениями, исследуются общими методами, разработка и применение которых составляет задачу теории колебаний.

Среди различных видов колебаний наиболее простой формой является гармоническое колебание, т.е. изменение физической величины по закону синуса или косинуса. То важное место, которое колебания занимают среди всех разнообразных форм колебаний, определяется двумя обстоятельствами. Во-первых, в природе и в технике очень часто встречаются колебательные процессы, по форме близкие к гармоническим колебаниям. Во-вторых, всякую периодическую, но не гармоническую функцию f (t) с частотой w можно разложить в гармонический спектр или совокупность простых гармонических колебаний, т.е. f(t) представить в виде ряда гармонических функций с частотами iw (i - номер гармоники), кратными основной частоте:

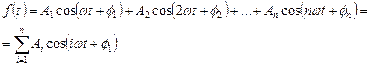
Рассмотрим случай, когда на систему кроме квазиупругой силы, возвращающей тело в положение равновесия и пропорциональной отклонению, и силы сопротивления среды (силы трения), никакие другие силы не действуют. В этом случае система будет совершать собственные свободные затухающие колебания. Второй закон Ньютона записывается в виде:

, (1)

где 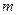— масса колеблющегося тела, 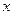— смещение, — коэффициент упругости пружины, — время.

Обычно предполагают, что при не очень больших амплитудах и частотах сила трения пропорциональна скорости движения и, естественно, направлена

противоположно скорости:

, (2)

где – коэффициент трения, характеризующий свойства среды оказывать сопротивление движению.

Подставляя (2) в (1), имеем: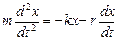

или , (3)

где , , - коэффициент затухания, – круговая частота собственных колебаний системы.

Решение уравнения (3) существенно зависит от знака разности .

Если w²-b²> 0, то w является действительной величиной и решение уравнения (3) имеет вид:

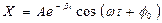, (4)

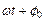где А – амплитуда свободного (собственного) гармонического колебания, – круговая частота затухающих колебаний системы, — начальная фаза, – фаза.

При отсутствии силы сопротивления среды () система совершает свободные незатухающие гармонические колебания. Такие колебания возникают вследствие начального смещения или начальной скорости и совершаются при отсутствии внешнего воздействия за счет первоначально сообщенной телу энергии. Уравнение (4) для данного случая принимает вид:

. (5)

Отметим, что частота колебаний n связана с круговой частотой следующим образом: , а период колебаний равен: .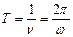

Графическое изображение свободных незатухающих гармонических колебаний представлено на рис. 1.

Характерная черта гармонических колебаний состоит в том, что скорость 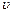и ускорение также изменяются гармонически:

,

где – амплитуда скорости,

,

где а₀ – амплитуда ускорения.

Кинетическая энергия колеблющейся материальной точки равна:

Потенциальная энергия колебательного движения находится из общей формулы для потенциальной энергии упругой деформации:

.

Полная механическая энергия колеблющейся материальной точки равна:

.

В отсутствие сил трения полная механическая энергия системы не изменяется (не зависит от времени):

.

Вернемся к случаю в уравнении (4), т.е. к затухающим колебаниям. График уравнения (4) в случае, когда b¹0, показан на рис. 2 сплошной кривой, пунктиром изображено изменение амплитуды.

Период затухающих колебаний зависит от коэффициента трения и определяется выражением:

.

При очень малом трении (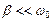) период затухающих колебаний близок к периоду незатухающих колебаний . Быстрота затухания колебаний определяется коэффициентом затухания: чем больше , тем сильнее тормозящее действие среды и тем быстрее уменьшается амплитуда. На практике степень затухания часто характеризуют логарифмическим декрементом затухания, т.е. натуральным логарифмом отношения двух амплитуд, разделенных интервалом времени, равным периоду колебаний:

.

Коэффициент затухания и логарифмический декремент затухания связаны соотношением:

.

Дата добавления: 2014-01-04