Сложение двух колебаний одинакового направления. Биения

Если два гармонических колебания происходят в одном направлении Х, имеют одинаковые периоды, но различные начальные фазы a₁ и a₂, то смещения X₁ и X₂ для этих двух колебаний можно записать в виде:

(3)

. (4)

Результирующее смещение ; действительно, если через некоторую точку 0 горизонтальной оси провести лучи под углами a₁ и a₂ к горизонтали и на этих лучах от точки 0 отложить амплитуды А₁ и А₂ слагаемых колебаний (рис. 3), то проекции амплитуд А ₁ и А ₂ на горизонтальную ось Х равны смещениям 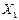и слагаемых колебаний.

Сложив векторно амплитуды A₁ и A₂ и спроецировав полученный вектор на ось ОХ, получаем результирующее смещение (рис. 3). Так как угол между векторами и все время остается постоянным (a=a₁-a₂), то векторный треугольник с течением времени не изменяет своей формы. Конец вектора в этом случае движется равномерно по окружности против часовой стрелки. Вектор результирующей амплитуды вращается с той же угловой скоростью 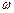, что и векторы амплитуд складываемых колебаний.

Проекция результирующего вектора на ось ОХ в каждый момент времени будет определять смещение результирующего колебания. Поэтому результирующее колебание является гармоническим и происходит по закону: .

Амплитуда этого колебания равна модулю вектора :

.

Если слагаемые колебания происходят по одному направлению, но с разными периодами, то результирующее колебание не является гармоническим. В этом случае векторы слагаемых колебаний и (рис. 3) вращаются с разными угловыми скоростями, в результате с течением времени: . Вследствие этого меняется и величина результирующей амплитуды А.

Обозначив круговые частоты слагаемых колебаний через w₁ и w₂ и приняв в качестве начального тот момент, при котором начальные фазы обоих колебаний одинаковы, эти колебания можно представить в следующем виде:

(5)

. (6)

Разность фаз колебаний (5) и (6) будет равна .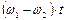

Амплитуда результирующего колебания:

. (7)

Из формулы (7) видно, что величина амплитуды А результирующего колебания меняется со временем, т.е. результирующее колебание не является гармоническим.

Если периоды и, следовательно, круговые частоты w₁ и w₂ мало отличаются друг от друга, то колебания в некоторые моменты времени оказываются почти совпадающими по фазе – в этот момент они “усиливают друг друга”. В другие моменты времени колебания оказываются почти противоположными по фазе - в этот момент времени они “гасят друг друга”.

При сложении двух колебаний с одинаковыми амплитудами А ₁= А ₂ абсолютное значение величины результирующей амплитуды определяется выражением:

. (8)

За промежуток времени аргумент косинуса в (8) изменится на величину p, т.е. , отсюда

. (9)

На основании выражения (9) частоту изменения амплитуды можно представить в виде:

, (10)

т.е. частота изменения амплитуды результирующего колебания равна разности частот слагаемых колебаний.

Угол, образованный результирующей амплитудой А с осью ОХ, равен , следовательно, вектор А вращается с угловой скоростью:

. (11)

Проецируя вектор результирующей амплитуды А на горизонтальную ось, получим результирующее смещение:

,

или

. (12)

Так как и близки по величине, то , поэтому результирующее колебание можно рассматривать как гармоническое колебательное движение, происходящее с круговой частотой, определяемой уравнением (11), амплитуда А которого, как это видно из уравнения (12), медленно меняется по закону . Этот вид колебаний называется биением (рис. 4). Время , называется периодом биений, а разность – угловой частотой биений. Токи, которые изменяются по указанной выше закономерности (рис. 4), называются синусоидальными модулированными токами. Синусоидальные модулированные токи широко используются в медицине для электростимуляции различных участков тела пациента. Для указанной цели используются аппараты “Амплипульс-3” и “Амплипульс-4”.

Дата добавления: 2014-01-04