Системы линейных уравнений с постоянными коэффициентами, методы их решения

Лекция 23.

Определение 23.1. Система дифференциальных уравнений называется линейной, если она линейна относительно всех неизвестных функций и их производных.

В частности, система линейных уравнений первого порядка с постоянными коэффициентами имеет вид:

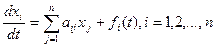. (23.1)

Можно использовать матричную запись такой системы, если ввести матрицы

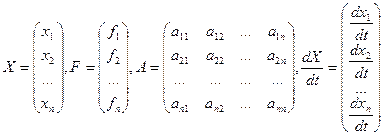. Тогда системе (23.1) эквивалентно матричное уравнение 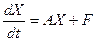. (23.2)

Если же рассмотреть линейный оператор 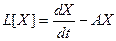, уравнение (23.2) примет вид:

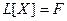. (23.3)

Так как оператор L обладает свойствами линейности:

1) L [ cX ] = cL [ X ];

2) L [ X₁ + X₂ ] = L [ X₁ ] + L [ X₂ ],

то для решений линейной однородной системы (23.3) (при F = 0) справедливы те же свойства: если Х₁ и Х₂ – решения однородного уравнения (23.3), то и их линейная комбинация будет решением того же уравнения.

Можно ввести понятие линейной зависимости решений Х₁, Х₂,…, Х_п:

Определение 23.2. Векторы (столбцы) Х₁, Х₂,…, Х_п, где

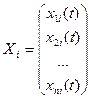, называются линейно зависимыми при 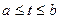, если существуют числа α₁,α₂,…, α _п, не все равные нулю, что

α₁Х₁ + α₂Х₂ +…+ α_пХ_п ≡ 0 (23.4)

при 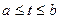. Если же тождество (23.4) справедливо только при всех α_i = 0, векторы называются линейно независимыми.

Замечание. Назовем определителем Вронского для уравнения (23.4) определитель вида

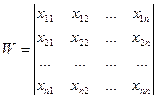, (23.5)

являющийся определителем системы уравнений, получаемых при координатной записи равенства (23.4). Можно показать, что так же, как и в случае решения линейного однородного уравнения, при W = 0 решения Х₁, Х₂,…, Х_п линейно зависимы на [ a,b ]. Тогда справедлива следующая теорема:

Теорема 23.1. Линейная комбинация 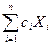п линейно независимых решений линейной однородной системы является общим решением этой системы.

Будем искать фундаментальную систему решений линейной однородной системы с постоянными коэффициентами

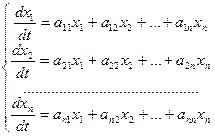(23.6)

в виде: 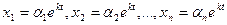, (23.7)

где α_i – постоянные. Подставив (23.7) в (23.6) и сократив на e^kt, получим:

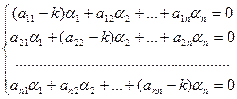. (23.8)

Для того, чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы ее главный определитель был равен нулю:

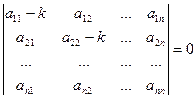, (23.9)

что представляет собой уравнение п – й степени относительно k, называемое характеристическим.

Если все корни характеристического уравнения различны, то, подставляя их последовательно в систему (23.8), можно найти соответствующие им значения 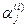и тем самым п различных решений системы (23.6). Эти решения линейно независимы. Действительно, если бы существовали числа β₁, β₂,…, β_п такие, что

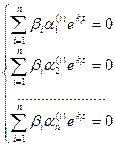, то в силу линейной независимости функций 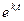отсюда следовало бы, что 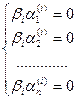для каждого i. Но поскольку хотя бы одно из 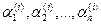не равно нулю, получаем, что все 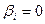. Следовательно, найденные решения (23.7) линейно независимы, и общее решение системы имеет вид: 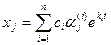, (23.10)

где c_i – произвольные постоянные.

Пример.

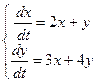. Составим характеристическое уравнение: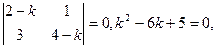

k₁ = 1, k₂ =5. Для k = 1 получаем систему для определения 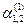: 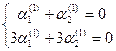, то есть

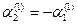. Примем 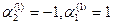, тогда 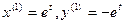. При k = 5 ,

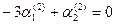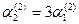. Тогда 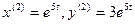. Следовательно, общее решение системы имеет вид: .

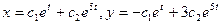В случае кратных корней характеристического уравнения решение системы (23.6) имеет вид

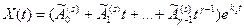, где γ – кратность корня k_s.

Пример.

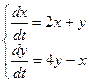. Характеристическое уравнение имеет вид: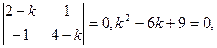

k₁ = k₂ = 3. Пусть x = (c₁ + c₂ t) e^3t, y = (c₃ + c₄ t) e^3t. Выразим постоянные с₃ и с₄ через с₁ и с₂. Для этого подставим найденные решения в одно из уравнений системы и приравняем коэффициенты при e^3t и te^3t: (3 c₁ + c₂ + 3 c₂t) e^3t = (2 c₁ + c₃) e^3t + (2 c₂ + c₄) te^3t, c₃ = c₁ + c₂,

c₄ = c₂. Итак, общее решение системы получено в форме: x = (c₁ + c₂ t) e^3t, y = (c₁+ с₂ + c₂t) e^3t.

Замечание. Для неоднородной системы (23.1) общим решением, так же как для неоднородного уравнения, будет сумма общего решения соответствующей однородной системы и частного решения неоднородной системы. При подборе частных решений справедлив принцип суперпозиции.

Пример.

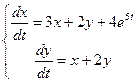. Найдем частное решение в виде: 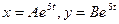. При подстановке получим: 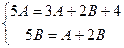, откуда А = 3, В = 1. Прибавив к полученному частному решению общее решение соответствующей однородной системы, запишем общее решение исходной системы: x = c₁e^t + 2 c₂e^4t + 3 e^5t, y = -c₁e^t + c₂e^4t + e^5t.

Дата добавления: 2013-12-12