
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функция двух переменных
|
|
|
|
Функции нескольких переменных
Тюмень, 2009
Высшая математика
Р.М. Султанаев
Кафедра математики, информатики и естественных наук
МИРОВОЙ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА
ТЮМЕНСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ
Высшего профессионального образования Тюменской области
Государственное образовательное учреждение
Курс лекций
для студентов всех специальностей
очной и заочной форм обучения
(ЧАСТЬ 2)
Лекция 1
Функции одной переменной не охватывают все зависимости существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных. В качестве примера функций нескольких переменных будем рассматривать функцию двух переменных, т.к. основные особенности таких многоаргументных зависимостей вполне проявляются и в этом случае.
Пусть задано множество D упорядоченных пар чисел (х;у),и соответственно f, которое каждой паре чисел (х;у) сопоставляет только одно число Z, f =Z называется функция двух непременных определенной на множество D и записывается в виде Z= f(х;у). При этом х и у называются независимыми переменными (аргументами),а Z зависимой переменной (функцией)., множество D – называется областью определения функции. Примером такой функции может служить площадь прямоугольника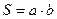 , треугольника
, треугольника 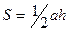 и т.д.
и т.д.
Функция двух переменных, как и функции одной переменной может быть задана разными способами (табличный, графический и аналитический). Мы, как правило, будем пользоваться аналитическим способом, когда функция задается с помощью формулы.
- Предел функции
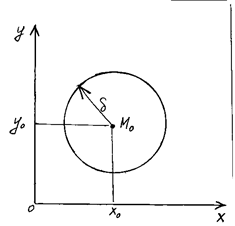 Это понятие вводится аналогично случаю одной переменной. Для этого надо ввести понятие окрестности точки, (δ-окрестность точки М0(х0,у0)). Это будут все внутренние точки круга с центром М0 и радиусом δ. Итак, пусть f(х; у) =.Z определена в некоторой окрестности точки М0(х0,у0), кроме, может быть, этой самой точки. Число А называется пределом Z= f(х; у) при х→х0 и у→у0, если для любого
Это понятие вводится аналогично случаю одной переменной. Для этого надо ввести понятие окрестности точки, (δ-окрестность точки М0(х0,у0)). Это будут все внутренние точки круга с центром М0 и радиусом δ. Итак, пусть f(х; у) =.Z определена в некоторой окрестности точки М0(х0,у0), кроме, может быть, этой самой точки. Число А называется пределом Z= f(х; у) при х→х0 и у→у0, если для любого 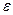 >0 существует δ>0, такое, что для всех х≠х0 и у≠у0 удовлетворяющих неравенству
>0 существует δ>0, такое, что для всех х≠х0 и у≠у0 удовлетворяющих неравенству 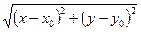 <δ выполняется неравенство │f(x,y)-A│<
<δ выполняется неравенство │f(x,y)-A│<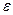 . Записывают:
. Записывают: 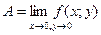 или
или 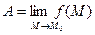
- Непрерывность функции двух переменных
Z= f(х; у) называется непрерывной в точке М0(х0,у0), если она:
а) определена в этой точке и некоторой ее окрестности.
б) имеет предел 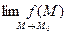
в) этот предел равен значению функции в точке М0, т.е. 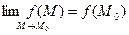
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается, называются точками разрыва этой функции. Точки разрыва могут образовывать целую линию разрыва. Так, функция 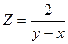 имеет линию разрыва у=х.
имеет линию разрыва у=х.
- Производные и дифференциалы функции нескольких переменных
а) частные производные первого порядка.
Пусть задана функция Z= f(х; у). Т.к. х и у – независимые переменные, то одна из них может меняться, а вторая сохранять свое значение. Дадим х приращение ∆х, сохраняя у=const. Тогда ∆хZ=f(x+∆x,y)-f(x,y). Аналогично получим ∆у Z=f(х,у+∆у)- f(x,y). Полное приращение функции ∆Z=f(x+∆x,у+∆y)-f(x,y). Если существует предел 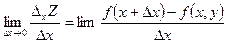 , то он называется частной производной функции Z= f(х;у) в точке М(х;у) по переменной х и обозначается Z′x,
, то он называется частной производной функции Z= f(х;у) в точке М(х;у) по переменной х и обозначается Z′x, 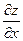 ;
; 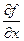 . Аналогично определяется и частная производная по у Z′=
. Аналогично определяется и частная производная по у Z′=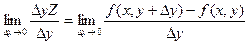 . Все частные производные находятся по формулам и правилам, полученным раннее для функций одной переменной и при условии, что или х или у – считаются const.
. Все частные производные находятся по формулам и правилам, полученным раннее для функций одной переменной и при условии, что или х или у – считаются const.
- Частные производные высших порядков
Если Z= f(х;у) имеет частные производные 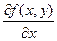 и
и 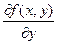 и они являются функциями от (х,у), то их можно продифференцировать и получить частные производные второго порядка
и они являются функциями от (х,у), то их можно продифференцировать и получить частные производные второго порядка 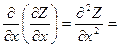 Z″xx;
Z″xx; 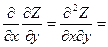 Z″xy;
Z″xy; 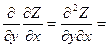 Z″yx и
Z″yx и 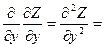 Z″yy; аналогичным образом можно ввести и определить частные производные 3, 4 и т.д. порядков. Частные производные, взятые по различным переменным, называются смешанными частными производными. Это Z″xy и Z″yx.
Z″yy; аналогичным образом можно ввести и определить частные производные 3, 4 и т.д. порядков. Частные производные, взятые по различным переменным, называются смешанными частными производными. Это Z″xy и Z″yx.
Теорема. Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой, т.е. Z″xy=Z″yx.
- Дифференцируемость и полный дифференциал функции
Пусть Z= f(х;у) определена в некоторой окрестности точки М(х;у) полное приращение ∆Z=f(x+∆x,у+∆у)-f(x,y). Z= f(х;у) называется дифференцируемой в М(х;у), если ее полное приращение можно представить в виде: ∆Z=А∆х+В∆у+α∆х+β∆у, где α= α(∆х,∆у)→0 и β= β(∆х,∆у)→0 при ∆х→0, ∆у→0. Сумма двух первых слагаемых представляет собой главную часть приращения функции. Главная часть приращения функции, линейная относительно ∆х и ∆у, называется полным дифференциалом функции и обозначается символом dZ=A∆x+B∆y. Выражения A∆x и B∆y называются частными дифференциалами. Для независимых переменных х и у полагают ∆x=dx, ∆y=dy. Поэтому dZ=Adx+Bdy.
Теорема 1. (необходимое условие дифференцирования функции). Если Z= f(х;у) дифференцируема в точке М(х;у), то она непрерывна в этой точке и имеет в ней частные производные 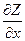 и
и 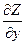 , причем
, причем 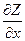 =А;
=А; 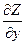 =В.
=В.
Таким образом, можно записать dZ=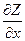 dx+
dx+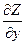 dy или dZ=dх Z+ dуZ.
dy или dZ=dх Z+ dуZ.
Теорема 2. Если Z= f(х; у) имеет непрерывные частные производные Z′х и Z′у в точке М (х;у), то она дифференцируема в этой точке и ее полный дифференциал выражается формулой записанной выше.
Чтобы функция Z= f(х; у) была дифференцируема в точке, необходимо чтобы она имела в ней частные производные и достаточно чтобы она имела в точке непрерывные частные производные.
Арифметические свойства правила исчисления дифференциалов функции одной переменной сохраняются и в случае дифференциалов функции двух и более переменных.
- Дифференциалы высших порядков
Полный дифференциал называется дифференциалом первого порядка. Пусть Z= f(х;у) имеет непрерывные частные производные второго порядка. Дифференциал второго порядка в этом случае определяется по формуле 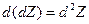 . Найдем ее d2 Z= d(
. Найдем ее d2 Z= d(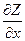 dx+
dx+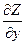 dy)= (
dy)= (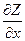 dx+
dx+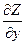 dy)х′ dx+(
dy)х′ dx+(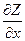 dx+
dx+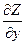 dy)у′ dу=(
dy)у′ dу=(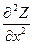 dx+
dx+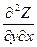 dy) dx+(
dy) dx+(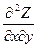 dx+
dx+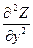 dy)dу, отсюда d2 Z=
dy)dу, отсюда d2 Z=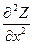 dx2+2
dx2+2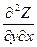 dx dy+
dx dy+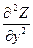 dy2. Символически это можно записать так: d2 Z=(
dy2. Символически это можно записать так: d2 Z=( )2Z. Аналогично можно получить формулу
)2Z. Аналогично можно получить формулу
d3 Z= d (d2 Z)==( )3Z, а для dn Z=(
)3Z, а для dn Z=( )nZ. Все эти соотношения справедливы лишь в случае, если переменные х и у функции Z= f(х;у) являются независимыми.
)nZ. Все эти соотношения справедливы лишь в случае, если переменные х и у функции Z= f(х;у) являются независимыми.
- Производная сложной функции. Полная производная
Пусть Z= f(х;у) – функция двух переменных х и у, каждая из которых является функцией независимой переменной t х=х(t),у=у(t). В этом случае Z= f(х(t);у(t)) является сложной функцией одной независимой переменной t, а переменные х и у – являются промежуточными переменными.
Теорема. Если Z= f(х;у) дифференцируема в точке М(х,у) и х=х(t),у=у(t) – дифференцируемые функции независимой переменной t, то производная сложной функции Z(t)= f(х(t);у(t)) вычисляется по формуле 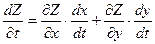 .
.
Доказательство. Дадим независимой t приращение ∆t. Тогда х=х(t) и у=у(t) получат приращения ∆х и ∆у соответственно. Они в свою очередь вызовут приращение ∆Z функции Z. Так как Z= f(х;у) по условию дифференцируемав М(х,у), то ее полное приращение равно ∆Z=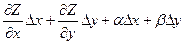 , где α→0 β →0 при ∆х→0 и ∆у→0. Разделим ∆Z на ∆t и перейдем к пределу ∆t→0, тогда ∆х→0 и ∆у→0 в силу непрерывности функций х=х(t); у=у(t) получаем:
, где α→0 β →0 при ∆х→0 и ∆у→0. Разделим ∆Z на ∆t и перейдем к пределу ∆t→0, тогда ∆х→0 и ∆у→0 в силу непрерывности функций х=х(t); у=у(t) получаем: 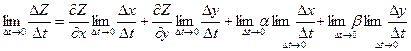 , т.е.
, т.е.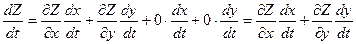 . Ч.т.д.
. Ч.т.д.
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 1485; Нарушение авторских прав?; Мы поможем в написании вашей работы!