Лекции №№2,3

Инвариантность формы полного дифференциала

Используя правила дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности, т.е. сохраняет один и тот же вид, независимо от того являются ли аргументы независимыми переменными или функциями независимых переменных.

Пусть Z= f(х;у), где x, y – независимые переменные, тогда полный дифференциал (1^ого порядка) имеет вид dZ=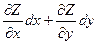

Рассмотрим сложную функцию Z= f(х; у), где x=x(u,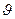), y=y(u,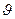), т.е. функция

Z= f(x(u,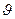), y(u,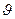))=F(u,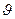), где u,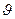- независимые переменные. Тогда имеем:

dZ=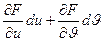==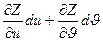(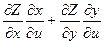)du+()d=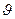

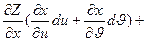
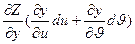
Выражения в скобках представляют собой полные дифференциалы dx и dy функции x=x(u,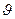) и y=y(u,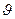). Следовательно, dZ=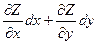

1. Дифференцирование неявной функции

Функция Z= f(х; у) называется неявной, если она задается уравнением F(x,y,z)=0 неразрешенным относительно Z. Найдем частные производные 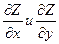функции Z заданной неявно. Для этого подставив в уравнение вместо Z функцию f(х;у) получим тождество F(x,y, f(х,у))=0. Частные производные по x и y функции, тождественно равной нулю, также равны нулю.

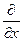F(x, y, f (х, у)) =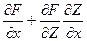=0 (y считаем постоянным)

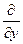F(x, y, f (х, у)) =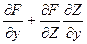=0 (x считаем постоянным)

Откуда 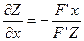и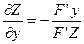

Пример: Найти частные производные функции Z заданной уравнением .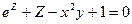

Здесь F(x,y,z)= 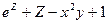; ; 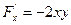; 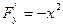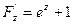. По формулам приведенным выше имеем:

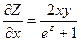и

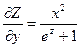
1. Производная по направлению

Пусть функция двух переменных Z= f(x; у) задана в некоторой окрестности т. М (x, y). Рассмотрим некоторое направление, определяемое единичным вектором 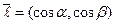, где (см. рис.).

На прямой, проходящей по этому направлению через т. М возьмем т. М₁ (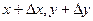) так, что длина 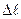отрезка MM₁ равна 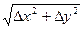. Приращение функции f(M) определяется соотношением 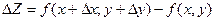, где 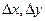связаны соотношениями 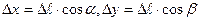. Предел отношения 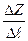при 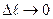будет называться производной функции 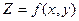в точке 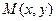по направлению 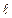и обозначаться .

=

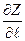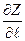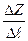
Если функция Z дифференцируема в точке 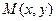, то ее приращение в этой точке с учетом соотношений для 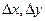может быть записано в следующей форме.

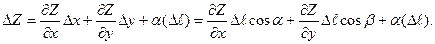поделив обе части на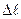

и переходя к пределу при 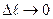получим формулу для производной функции Z= f(х; у) по направлению:

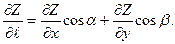
1. Градиент

Рассмотрим функцию трех переменных 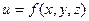дифференцируемой в некоторой точке .

Градиентом этой функции 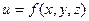в точке М называется вектор, координаты которого равны соответственно частным производным 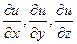в этой точке. Для обозначения градиента используют символ .=.

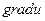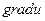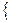
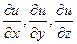
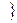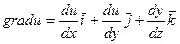.Градиент указывает направление наибыстрейшего роста функции в данной точке.

Поскольку единичный вектор 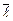имеет координаты (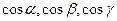), то производная по направлению для случая функции трех переменных записывается в виде , т.е. 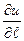имеет формулу скалярного произведения векторов 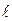и 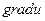. Перепишем последнюю формулу в следующем виде:

, где 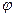- угол между вектором 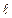и 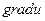. Поскольку 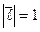, то отсюда следует, что производная функции по направлению принимает max значение при 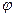=0, т.е. когда направление векторов 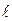и 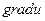совпадают. При этом 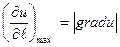.Т.е., на самом деле градиент функции характеризует направление и величину максимальной скорости возрастания этой функции в точке.

1. Экстремум функции двух переменных

Понятия max, min, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной переменной. Пусть функция Z= f(x; у) определена в некоторой области D и т. М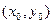принадлежит к этой области. Точка М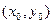называется точкой max функции Z= f(x; у), если существует такая δ-окрестность точки 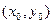, что для каждой точки из этой окрестности выполняется неравенство 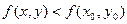. Аналогичным образом определяется и точка min, только знак неравенства при этом изменится 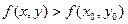. Значение функции в точке max (min) называется максимумом (минимумом). Максимум и минимум функции называются экстремумами.

1. Необходимые и достаточные условия экстремума

Теорема: (Необходимые условия экстремума). Если в точке М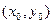дифференцируемая функция Z= f(x; у) имеет экстремум, то ее частные производные в этой точке равны нулю: ,.

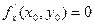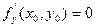Доказательство: зафиксировав одну из переменных x или y, ревратим Z= f(x; у) в функцию одной переменной, для экстремума которой вышеописанные условия должны выполняться. Геометрически равенства 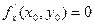и 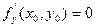означают, что в точке экстремума функции Z= f(x; у), касательная плоскость к поверхности, изображающую функцию f(x,y)=Z параллельна плоскости OXY, т.к. уравнение касательной плоскости есть Z=Z_0. Точка, в которой частные производные первого порядка функции Z= f(x; у) равны нулю, т.е. 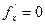,,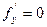 называются стационарной точкой функции. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например Z=|-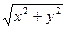| имеет max в точке O(0,0), но не имеет в этой точке производных.

Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Например, при Z=xy точка O(0,0) является критической. Однако экстремума в ней функция Z=xy не имеет. (Т.к. в I и III четвертях Z>0, а в II и IV – Z<0). Таким образом для нахождения экстремумов функции в данной области необходимо подвергнуть каждую критическую точку функции дополнительному исследованию.

Теорема: (Достаточное условие экстремумов). Пусть в стационарной точке 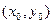и некоторой окрестности функция f(x; у) имеет непрерывные частные производные до 2^ого порядка включительно. Вычислим в точке 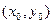значения 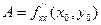,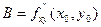и . Обозначим

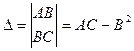
Тогда:

1) если 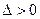, то f(x; у) в точке 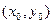имеет экстремум max, если А<0 и min, если А>0.

2) если , то f(x; у) в точке 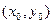экстремума не имеет.

В случае если 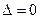, экстремум в точке 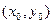может быть, а может и не быть. Необходимы дополнительные исследования.

Дата добавления: 2013-12-12