
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расстояние от точки до плоскости
|
|
|
|
Взаимное расположение плоскостей в пространстве.
Рассмотрим плоскости 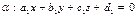 и
и 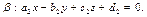 Их взаимное расположение характеризуется углом между ними. Этот угол однозначно определяется углом между нормальными векторами этих плоскостей
Их взаимное расположение характеризуется углом между ними. Этот угол однозначно определяется углом между нормальными векторами этих плоскостей 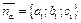 и
и 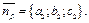 Обозначим через
Обозначим через 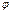 - угол между нормальными векторами. Тогда:
- угол между нормальными векторами. Тогда:
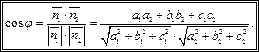 (14.8)
(14.8)
Замечание. Обратим внимание, что угол между плоскостями не обязательно равен 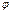 , он может быть равен и
, он может быть равен и 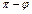 (рис. 14.4-14.5).
(рис. 14.4-14.5).
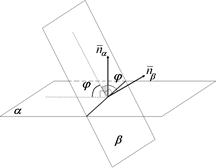 Рис. 14.4 Рис. 14.4
| 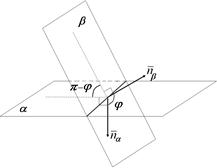 Рис. 14.5 Рис. 14.5
|
Таким образом, формула (14.8) определяет значение косинуса угла между плоскостями с точностью до знака. Косинус острого угла между плоскостями 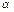 и
и 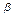 может быть найден по формуле:
может быть найден по формуле:
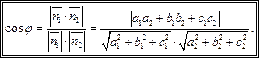 (14.9)
(14.9)
Заметим, что 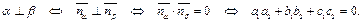
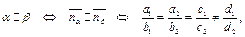
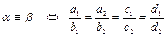 .
.
Пусть в пространстве задана плоскость 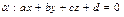 и точка и точка 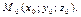 Найдем расстояние от точки Найдем расстояние от точки 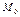 до плоскости до плоскости 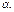 Очевидно, что какова бы ни была точка Очевидно, что какова бы ни была точка 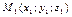 плоскости плоскости 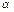 (рис. 14.6), справедливо соотношение: (рис. 14.6), справедливо соотношение:
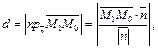 где где 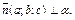
| 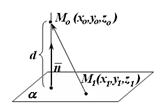 Рис. 14.6
Рис. 14.6
|
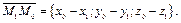 Поскольку
Поскольку 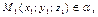 то
то
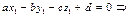
 Тогда:
Тогда: 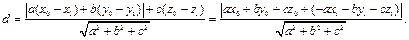
Таким образом, имеем:
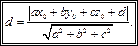 (14.10)
(14.10)
Замечание. Если нормальный вектор плоскости 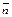 отложен от некоторой точки прямой, то для всех точек
отложен от некоторой точки прямой, то для всех точек 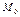 , которые лежат в одной полуплоскости с концом вектора
, которые лежат в одной полуплоскости с концом вектора 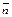
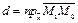 , а для всех точек, лежащий в другой полуплоскости,
, а для всех точек, лежащий в другой полуплоскости, 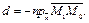 Таким образом, для точек, лежащих в одной из полуплоскостей, на которые разбивает координатную плоскость прямая,
Таким образом, для точек, лежащих в одной из полуплоскостей, на которые разбивает координатную плоскость прямая, 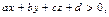 а для точек другой полуплоскости
а для точек другой полуплоскости 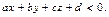
N. Две грани куба лежат в плоскостях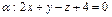 и
и 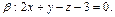 Найти объем куба.
Найти объем куба.
Решение.
Т.к. 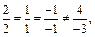 то
то 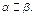 Значит, в условии речь идет о противоположных гранях куба. Ребро куба
Значит, в условии речь идет о противоположных гранях куба. Ребро куба 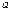 равно расстоянию между этими плоскостями. Для его нахождения выберем произвольную точку плоскости
равно расстоянию между этими плоскостями. Для его нахождения выберем произвольную точку плоскости 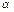 и вычислим расстояние от нее до плоскости
и вычислим расстояние от нее до плоскости 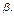
Пусть точка 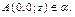 Значит, ее координаты удовлетворяют уравнению плоскости
Значит, ее координаты удовлетворяют уравнению плоскости 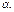
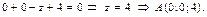
Найдем расстояние от точки 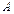 до плоскости
до плоскости 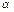 по формуле (14.10).
по формуле (14.10).
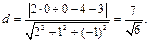 Таким образом,
Таким образом, 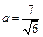 и
и 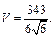
Ответ. 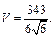
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 619; Нарушение авторских прав?; Мы поможем в написании вашей работы!