Уравнение баланса энергии подвижного потока (уравнение Д. Бернулли). Уравнение неразрывности подвижного потока (уравнение Л

Уравнение неразрывности подвижного потока (уравнение Л. Эйлера)

Уравнение неразрывности отражает условие сохранения массы движущегося потока жидкости или газа. Для вывода уравнения мысленно выделим в потоке жидкости или газа замкнутый объём в виде трубки тока:

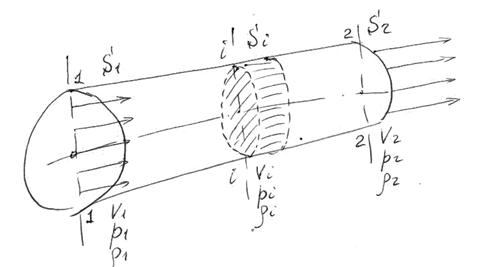
Рис 2.3.1 Схема трубки тока движущегося потока

Уравнение неразрывности выведено на основании закона сохранения материи, уста-новленного в 1748 г. русским ученным М.В. Ломоносовым. Уравнение неразрывности бы-ло опубликовано Л. Эйлером в 1770 г. и представляет собой применение закона сохране-ния энергии к струйке газа.

Пусть в сечении “ 1-1 ” площадь 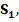параметры состояния газа равны 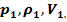За время 1с через сечение проходит масса воздуха

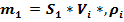
Через сечения “2–2” проходит за 1с своя масса воздуха .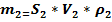

Так как через боковую поверхность трубки тока воздух не просачивается, то через любое сечение трубки за одинаковое время проходит одинаковая масса воздуха.

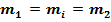или

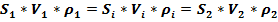= const

Тогда для установившегося движения уравнение имеет вид:

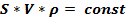, или S = const /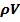

Где

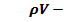удельный расход газа;

При небольших скоростях прямолинейного поступательного движения воздуха сжи-маемостью можно пренебречь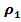 = 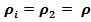, тогда уравнение примет вид:

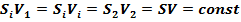
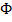изический смысл уравнения: при малых скоростях движения воздуха уменьшение площади поперечного сечения потока вызывает увеличение скорости движения.

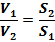
Отсюда

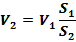
Из уравнения следует, что при дозвуковой скорости потока скорость движения газа в струйке обратно пропорционально площади поперечного сечения, т.е. при уменьшении площади поперечного сечения струйки скорость течения возрастает, и наоборот.

В случае движения с большой дозвуковой, трансзвуковой и сверхзвуковой скорос-тью, когда проявляется свойство сжимаемости 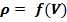, изменение скорости зависит не только от площади поперечного сечения, но и от изменения плотности. Тогда выражение примет вид:

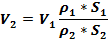
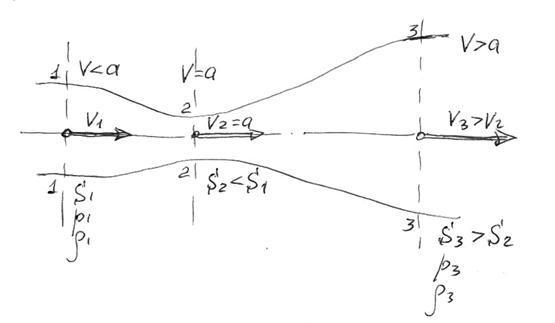
При сверхзвуковой скорости потока вследствие особенностей изменения физических характеристик плотность газа меняется быстрее, чем скорость. Поэтому для получения сверзвуковой скорости и ее увеличения необходимо расширять струйку, увеличивать ее площадь поперечного сечения по определенному закону. Непрерывное увеличение ско-рости потока от дозвуковой до сверхзвуковой возможно лишь в струйке, имеющей форму сопла Лаваля.

При больших скоростях потока на сжимаемость воздуха оказывает влияние не только скорость потока, но и скорость звука в потоке. В качестве критерия сжимаемости движущегося воздуха используется число Маха 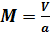. Чем больше скорость потока воздуха тем больше его сжимаемость.

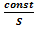V= V=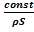

Рис 2.3.2 Схема течения потока вздуха в сопле Лаваля

Таким образом, уравнение постоянства расхода, являясь частным выражением зако-на сохранения материи применительно к струйке газа, связывает между собой скорость, плотность и площадь того поперечного сечения струйки, в котором рассматриваються эти характеристики.

ЛЕКЦИЯ 2.4 УРАВНЕНИЯ СОХРАНЕНИЯ И БАЛАНСА ЭНЕРГИИ ПОДВИЖНОГО ГАЗОВОГО ПОТОКА. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ОСНОВНЫХ УРАНЕНИЙ АЭРОГИДРОГАЗОДИНАМИКИ

План:

2.4.1 Уравнения сохранения энергии движущегося газового потока

Дата добавления: 2013-12-12