Вращательное движение вокруг неподвижной оси

Поступательное движение

ДИНАМИКА ТВЕРДОГО ТЕЛА

Дифференциальные уравнения различных типов движений твердого тела можно получить, применяя соответствующие теоремы динамики.

Из теоремы о движении центра масс получаются дифференциальные уравнения поступательного движения твёрдого тела. Из кинематики известно, что при поступательном движении все точки имеют одинаковые характеристики (скорость, ускорение), следовательно, движение тела определяется движением одной точки, За такую точку целесообразно принять центр масс системы. Тогда на основании теоремы получим

,

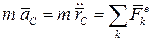где 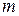— масса твердого тела.

Проектируя на оси системы координат, получаем дифференциальные уравнения поступательного движения

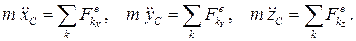
Таким образом, изучение поступательного движения твердого тела сводится к изучению движения одной точки.

Рассмотрим твёрдое тело, вращающееся вокруг неподвижной оси. Угловую скорость его вращения в произвольный момент времени обозначим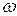. Тогда кинетический момент этого тела относительно оси 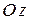равен

.

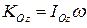Учитывая постоянство момента инерции для твёрдого тела, согласно теореме об изменении кинетического момента имеем

.

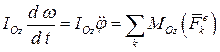Это и есть дифференциальное уравнение вращательного движения твёрдого тела вокруг неподвижной оси.

Частные случаи:

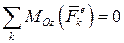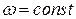· если, то, т.е. вращение равномерное;

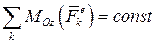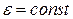· если, то, т.е. вращение равнопеременное.

Следует отметить, что дифференциальное уравнение вращательного движения аналогично по структуре дифференциальному уравнению поступательного движения твёрдого тела, откуда следует, что момент инерции во вращательном движении играет ту же роль, что и масса в поступательном движении, т.е. он характеризует инерционные свойства тела во вращательном движении. В этом смысле момент внешних сил аналогичен силам в поступательном движении.

Дата добавления: 2013-12-12