Сферическое движение твердого тела

Плоское движение

Из кинематики известно, что плоское движение твёрдого тела можно разложить на два простейших: поступательное вместе с полюсом и вращательное вокруг полюса. Примем за полюс центр масс тела. Тогда кинематические уравнения плоского движения запишутся в виде:

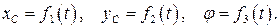
Для изучения плоского движения твёрдого тела достаточно составить три дифференциальных уравнения, связывающие величины 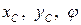с действующими на тело внешними силами.

Поступательная часть движения определяется дифференциальным уравнением поступательного движения (теоремой о движении центра масс)

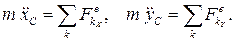
Третье уравнение плоского движения получим, применив теорему об изменении кинетического момента относительно подвижной оси, проходящей через центр масс

.

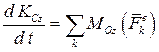Так как кинетический момент твёрдого тела относительно оси 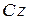можно определить по формуле 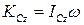то, подставляя его в теорему, получим

.

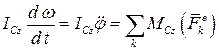Таким образом, дифференциальные уравнения плоского движения твёрдого тела имеют вид

.

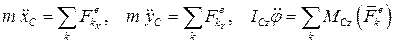Твердое тело с одной неподвижной точкой имеет три степени свободы. Классическими параметрами, определяющими положение этого тела в пространстве, являются три угла Эйлера: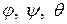. Если 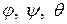известны как функции времени, то известно и движение твердого тела с одной неподвижной точкой (сферическое движение) (рис. 3.6).

Для составления дифференциальных уравнений сферического движения запишем теорему об изменении кинетического момента в дифференциальной форме

,

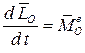где 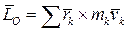— кинетический момент твердого тела, совершающего сферическое движение относительно неподвижной точки;

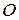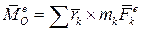— главный момент внешних сил относительно неподвижного центра.

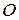Чтобы записать соответствующие формулы в наиболее простом виде возьмем в качестве координатных – подвижные главные оси инерции 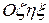жестко связанные с телом. Тогда проекции кинетического момента на оси координат можно записать в виде

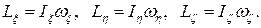
Уравнения движения (динамические уравнения Эйлера) в этом случае примут вид:

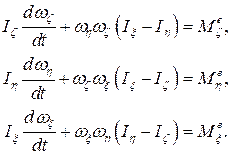
где 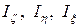– моменты инерции тела относительно его осей инерции в точке О;

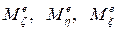– главные моменты внешних сил, приложенных к телу, относительно этих же осей.

К динамическим уравнениям Эйлера следует присоединить кинематические уравнения Эйлера:

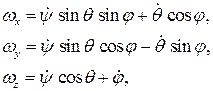
которые выражают проекции вектора угловой скорости вращения твердого тела на оси подвижной системы координат, скрепленные с телом через углы Эйлера и их производные по времени.

Рис. 3. 6 Сферическое движение твердого тела.

Динамические и кинематические уравнения Эйлера образуют систему шести нелинейных дифференциальных уравнений первого порядка; интегрирование этой системы представляет сложную математическую задачу. Для интегрирования этих уравнений при решении конкретных задач обычно используют те или иные приближенные математические методы.

Дата добавления: 2013-12-12