Сложение взаимно перпендикулярных колебаний

Биение

Сложение гармонических колебаний одного направления

Предполагаем что имеется два колебания одного направления имеющие одинаковые частоты, но различные амплитуды и фазы. В процессе колебания происходит взаимосвязь выражения этих двух колебательных движений. Определяя вид движения которого полученного в результате взаимного наложения этих колебаний. Для этого воспользуемся методом векторных диаграмм. Сущность: каждое из колебаний можно изобразить в виде вращающегося вектора будет определять амплитуду колебания угловая скорость вращения вектора циклическую частоту, а углом между некоторым началом отсчёта и положением вектора определяют фазу колебания в данный момент времени.

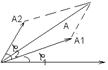
Сумма этих векторов даст нам вектор. Таким образом используя метод векторных диаграмм сделали вывод что в результате наложения двух колебаний распространяющихся в одном направлении получили колебание частота которого равна частоте двух накладывающихся колебаний. Если частоты равны. Амплитуда данного колебания определяется

Фаза определяется:

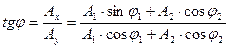
Биением называется колебания которые получаются в результате наложения двух колебаний с близкими частотами и одинаковыми амплитудами.

В результате наложения этих двух квази моно хроматических колебаний получаем колебание.

Таким образом в результате наложения двух колебаний с близкими частотами получаем колебание амплитуда которого меняется по гармоническому закону. Полученное выражение даст возможность изобразить х – колебаний биений.

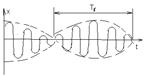
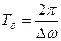
Биение (эффект биений) используется для поверки генераторов.

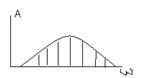
Явление сложения колебаний используется в современной радиотехнике и в современной системе передачи сигналов а так же в системе анализа спектров сигнала. Любой сложный сигнал можно разложить по спектральной составляющей в основе данного разложения лежит математический аппарат рядов Фурье. То есть сигнал колебаний сложной Фомы можно представит как сумму гармонических колебаний с частотами кратной некоторой частоте

Чем больше гармонических составляющих взять тем более точно можно взять некий сложный сигнал, через его гармоническую составляющую.

Имеется два колебания с одинаковой частотой но разной амплитуды, причём данные колебания происходят в двух взаимно перпендикулярных колебаний х и y.

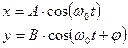
Разность фаз определяется как .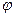

Рассмотрим вид движения который получился от взаимного наложения этих колебаний друг на друга.

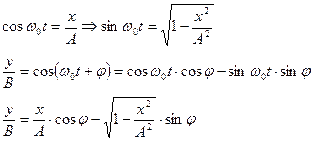
Полученное уравнение представляет из себя уравнение эллипса. Это говорит о том что конец вектора изображает результирующее колебание в плоскости x, y. Описывает эллипс. То есть результат колебания является поляризованным то есть упорядоченным в пространстве. Причём размер эллипса и его ориентация относительно оси x, y зависит от амплитуд колебаний. И от разности фаз этих двух колебаний.

Можно показать что в том случае разность фаз (-целое число), то в этом случае эллиптически поляризованные колебание преобразуется в линейные поляризованные колебания.

В том случае если разность фаз будет кратно 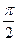то результирующее колебание будет являться эллипсом ориентированным вдоль оси x, y причём полу оси этого эллипса А и В

Соответствует амплитудам первого и второго колебания.

При наложении двух колебаний распространяющихся во взаимно перпендикулярных направлениях, но с различными частотами получается колебание конец вектора которого описывает фигуру листажу.оляризованные колебание преобразуется в линейное п то есть упорядоченным в пространстве. роисходят в двух взаимно перпендикуляр

Дата добавления: 2013-12-12