АЧХ вынужденных колебаний

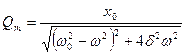
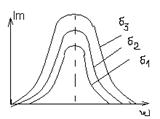
Полученное выражение для амплитуды заряда вынужденных колебаний является функцией зависящей от частоты. Анализ данного выражения даёт возможность построить АЧХ вынужденных колебаний заряда на ёмкости.

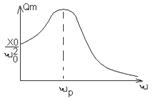Исследование данной функции на экстремум показывает что на частоте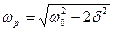у функции существует ярко выраженный максимум.

На частоте 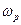наблюдается резкое увеличение амплитуды вынужденных колебаний. Данное явление получило название резонанса.

Резонансом называется явление резкого увеличения амплитуды колебаний при совпадении частоты внешнего воздействия с резонансной частотой колебательной системы.

Определим во сколько раз будет увеличиваться амплитуда вынужденного колебания на резонансной частоте по сравнению с амплитудой колебания на нулевой частоте. Подставляя выражение для резонансной частоты в выражение для 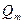получаем что:

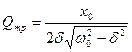
При малых затуханиях, если 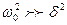выражение для амплитуды заряда на резонансной частоте может быть записано следующим образом:

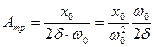
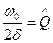- добротность колебательной системы

Таким образом на резонансной частоте происходит увеличение амплитуды вынужденного колебания по сравнению с амплитудой на нулевой частоте в .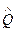

Анализ выражения для 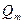и для резонансной частоты показал что данные величины зависят от 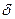(коэффициента затухания). С увеличением 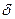происходит уменьшение резонансной частоты и уменьшение амплитуды вынужденного колебания на резонансной частоте.

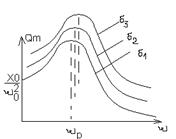Данный анализ даёт возможность построить графики АЧХ при различных .

Полученное выражение даёт возможность построить АЧХ для амплитуды тока:

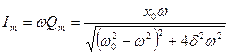
Исследование данной функции на экстремум показал, что на частоте 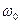наблюдается резкое увеличение амплитуды тока. Подстава 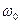в выражение для 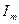позволяет определить амплитуду тока на резонансной частоте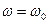

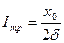
Как видно величина тока на резонансной частоте (амплитуда тока) уменьшается.

Важной характеристикой колебательного контура как селективной системы является полоса пропускания данного колебательного контура.

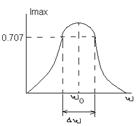ПП определяет тот частотный интервал 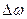в близи резонансной частоты взятый на уровне 0,707 от максимального значения тока на АЧХ тока в колебательном контуре. Чем уже ПП тем более избирательный и селективный является контур. Можно показать что полоса пропускания колебательного контура обратно пропорциональна добротности. То есть чем выше добротность, тем более селективным является контур.

Дата добавления: 2013-12-12