Вынужденные колебания

Как было показано выше все реальные колебания являются затухающими. То есть если в гармоническом осцилляторе была накоплена энергия и за счёт данной накопленной энергии происходит колебание, то с течением времени данное колебание затухает и его амплитуда уменьшается по экспоненте. Для поддержания колебательного процесса в некоторой колебательной системе необходимо на данную колебательную систему необходимо воздействовать внешней периодически меняющейся силой. Рассмотрим процесс вывода дифференциального уравнения вынужденных колебаний на примере пружинного маятника совершающего колебания в среде с потерями. Предполагаем что на пружинный маятник будет действовать как упругая сила так и сила сопротивления, которая пропорциональна скорости.

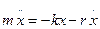
Данное дифференциальное уравнение представляет собой запись второго закона Ньютона в проекции на ось х.

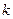- жёсткость пружины;

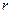- коэффициент сопротивления;

Для поддержания колебательного процесса. На данный осциллятор необходимо воздействовать с помощью внешней периодически меняющейся силы.

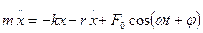
Можно перейти к дифференциальному уравнению

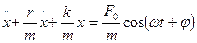
Если ввести следующее обозначение:

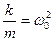- собственная частота свободного колебания;

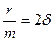- коэффициент затухания.

То последнее выражение преобразовывается к виду:

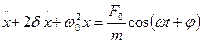
Данное уравнение является дифференциальным уравнением вынужденных колебаний пружинного маятника.

Вынужденные колебания можно получить в колебательном контуре, если включить в колебательную систему источник переменного напряжения изменяющегося по гармоническому закону.

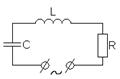Исходя из второго правила Кирхгофа для величины заряда на ёмкости, можно получить следующее дифференциальное уравнение:

(*)

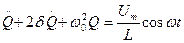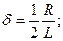
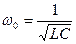
Данное дифференциальное уравнение является дифференциальным уравнением второго порядка, неоднородным со специальной правой частью. Общее решение данного уравнения можно представить в виде двух слагаемых.

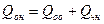
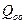- решение однородного уравнения;

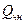- частное решение не однородного уравнения;

Общее решение однородного уравнения было найдено выше оно описывает не затухающие однородные колебания.

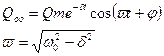
Частное решение неоднородного дифференциального уравнения ищется методом подстановки Эйлера. Согласно данному методу: в исходном дифференциальном уравнении правая часть заменяется комплексным числом реальная часть которого равна правой части исходного дифференциального уравнения. Решая дифференциальное уравнение находим его решение в виде комплексной функции и взяв реальную часть у полученного решения определяем последнюю как решение исходного дифференциального уравнения (*).

Данная методика основана на том, что все операции над комплексными числами выполняются отдельно над реальной и отдельно над мнимой частью. Следовательно уравнение (*) запишем:

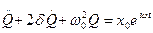(1)

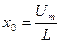
Решение данного уравнения будем искать в следующем виде:

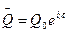
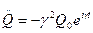
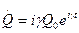
Подставляем в уравнение (1) получаем:

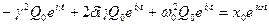(2)

Данное уравнение имеет решение в том случае если 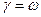, где 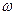- частота внешнего напряжения поданного на данный колебательный контур.

С учётом последнего (2) переписываем:

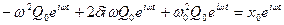
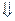
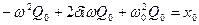
Отсюда

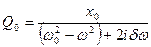
Таким образом решение получили в виде комплексного числа. Выделим реальную часть. Для этого числитель и знаменатель умножим на число комплексно сопряжённое с выражением для знаменателя.

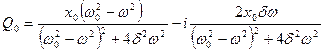
Любое комплексное число можно представить в следующем виде:

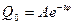
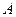- амплитуда;

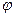- фаза;

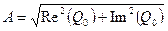
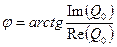
Подставляем реальную и мнимую часть в выражение для 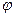и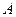

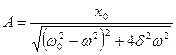
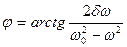
Таким образом решение исходного уравнения (*) может быть записано следующим образом:

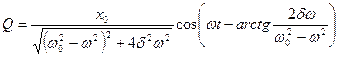
Полученное частное решение неоднородного дифференциального уравнения позволяет построить график вынужденных электрических колебаний.

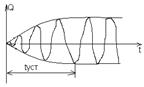На данном графике можно выделить время установления вынужденных колебаний. В течении этого времени устанавливается амплитуда вынужденных колебаний. Амплитуда достигает значения равного А.

В течении этого времени установления доминирующую роль играют свободные затухающие колебания которые описываются функцией являющейся общим решением однородного дифференциального уравнения. Через время установления доминирующую роль начинают играть вынужденные колебания с амплитудой А. Вынужденные колебания являются квази периодическими. Строго говоря периодическими их назвать нельзя.

Как видно из выражения описывающего частное решение неоднородного дифференциального уравнения: амплитуда вынужденных колебаний является функцией зависящей от частоты. Используя введённое ранее соотношение:

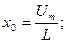
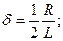
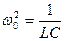
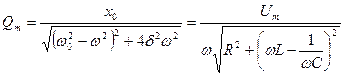
Выражение фигурирующее под знаком радикала получило название полного сопротивления электрической цепи или эмпиданса.

Эмпиданс состоит из активной части (R) и реактивной части, которая состоит из индуктивного сопротивление и ёмкостного сопротивления. Индуктивное сопротивление 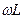- это частотно зависимое сопротивление и как видно прямо пропорционально частоте. Ёмкостное сопротивление так же является частотно зависимым сопротивлением и обратно пропорционально частоте .

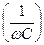Фазу вынужденных колебаний 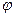так же можно выразить через параметры электрической цепи.

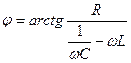
Получив выражение для величины заряда можно определить ток протекающий в данной электрической цепи.

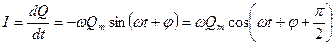
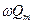- амплитуда тока;

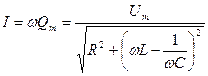
Как следует из выражения для тока. Ток в данной электрической цепи опережает на 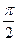напряжение на емкости (заряд на ёмкости).

Дата добавления: 2013-12-12