Частное решение неоднородного уравнения

Решение дифференциального уравнения

Дифференциальное уравнение, описывающее вынужденные колебания

наших двух систем будет иметь один и тот же вид:

.

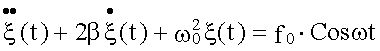Решение дифференциального уравнения вынужденных колебаний - ξ(t) - состоит из двух слагаемых:

,

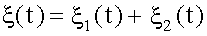здесь ξ₁(t) - общее решение однородного уравнения, т.е. уравнения с нулем в правой части (см. 14.4.5.),

ξ₂(t) - частное решение неоднородного уравнения, т.е. уравнения с ненулевой правой частью - (14.5.5)

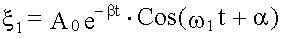- из (14.4.6),

здесь - 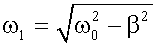- частота затухающих колебаний.

ξ₁(t) убывает с течением времени и его роль существенна при переходных процессах. Стационарное, установившееся значение ξ(t) определяется, в основном, слагаемым ξ₂(t). Наша задача - найти ξ₂(t).

Частное решение неоднородного уравнения - ξ₂(t). Ищем ξ₂(t) в виде гармонической функции изменяющейся с частотой внешнего воздействия ω:

.

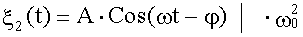Первая и вторая производные от этой функции также будут гармоническими функциями, изменяющиеся с частотой ω. Значит, в уравнении 14.5.3.5, в левой его части, будет сумма трех гармонических функций одинаковой частоты, справа - гармоническая функция той же частоты, т.е. сумма трех колебаний одной частоты равна четвертому колебанию той же частоты. Задачу о сложении колебаний мы решим методом векторных диаграмм (14.3.1.), для этого и , после нахождения этих производных, запишем с помощью функции косинуса:

.

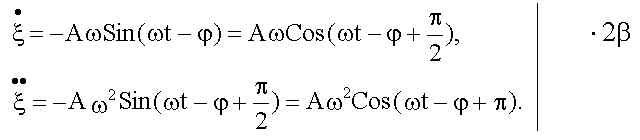14.5.6.1.1. Векторная диаграмма

Изобразим эти колебания с помощью векторов (14.3.1.), амплитуды которых получаются после умножения 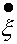на 2β, а - ξ на ω²₀.

.

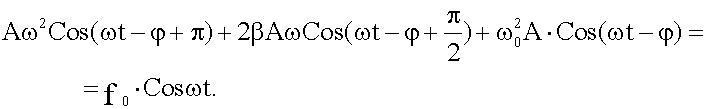В отличие от (14.3.2) вправо направим вектор длиной ω²₀A, изображающий функцию ω²₀A · Cos(ωt - φ), начальная фаза которой равна "минус фи".

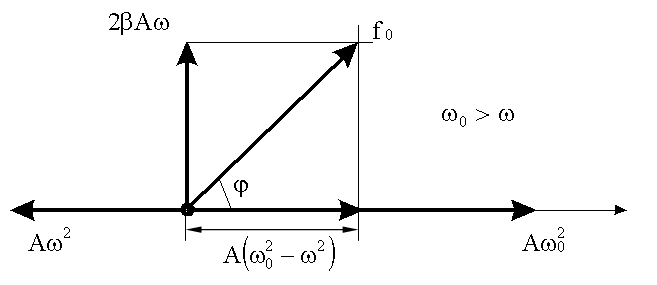
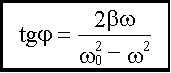
14.5.6.1.2. Резонанс

Т.к. ,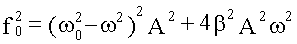

то

.

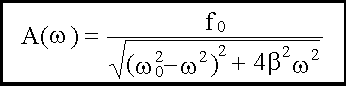Таким образом, амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определенной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота - ω_рез - резонансной. Для определения ω_рез исследуем функцию A(ω) на максимум, для этого достаточно найти минимум знаменателя у выражения A(ω). Возьмем от него производную по и приравняем к нулю:

,

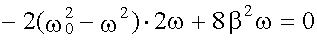откуда:

.

При 2β² > ω²₀ резонанс отсутствует (ω_рез - мнимое число).

14.5.6.1.2.1. Амплитуда при резонансе

Амплитуда при резонансе получается при подстановке найденного выражения ω_рез в формулу для A(ω).

.

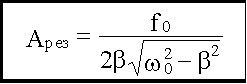При β << ω₀:

.

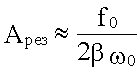При ω = 0 отклонение системы от положения равновесия

.

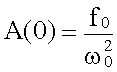Найдем отношение A_рез / A₀ при условии β << ω₀:

,

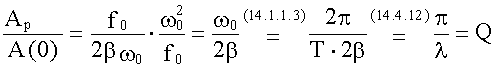здесь Q - добротность.

Добротность показывает (при β << ω₀) во сколько раз амплитуда при резонансе больше смещения при ω = 0.

14.5.6.1.2.2. Резонансные кривые

График зависимости A(ω) при различных β носят название резонансных кривых.

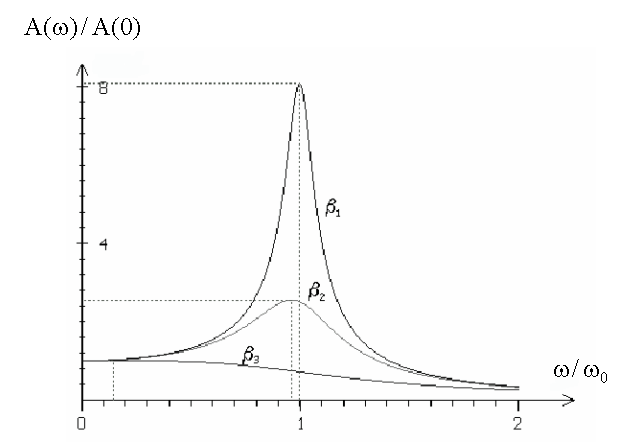
β₁ < β₂ < β₃, 2β²₃ > ω²₀, в этом случае резонанса нет.

Дата добавления: 2013-12-12