Энтропия. Рассмотрим процесс расширения газа

Необратимые процессы

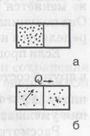Рассмотрим процесс расширения газа. Пусть имеется сосуд с перегородкой (рис. а) в левой части которого есть газ, а в правой – нет. Уберем перегородку. Газ расширится и займет обе части. Если молекулы друг с другом не взаимодействуют (идеальный газ), то общая внутренняя энергия при таком процессе не изменится (U_I =U_II). Однако со­стояние II отличается от состояния I тем, что тело из состояния II самопроизвольно, без вмешатель­ства извне не вернется в состояние I. Если молекул мало, например 2 или 3, то, двигаясь хаотически, случайно, они все могут в какой-то момент оказать­ся в левой части, но если молекул много, то это крайне маловероятно. Поэтому процесс расширения газа в пустоту называют необратимым.

Другой пример: пусть газ находится и слева и справа от теплопроводной пе­регородки, но температура слева выше, чем температура спра­ва (рис. б). Молекулы обмениваются с перегородкой кинетической энергией, и постепенно тем­пературы обеих частей выравниваются. Такой процесс передачи тепла всегда необратим. Самопроизвольно средняя кинетиче­ская энергия молекул (т. е. температура) слева сама не подни­мется за счет кинетической энергии молекул справа.

Любой процесс, сопровождающийся трением, также необ­ратим, так как при этом энергия упорядоченного движения пе­реходит в энергию беспорядочного движения молекул, т. е. в теплоту.

Пусть с рабочим веществом совершаются циклы, при каж­дом из которых подводится от нагревателя Q₁, отдается холо­дильнику Q₂ и производится работа

А = Q₁ – Q₂. Из (38) и (39) можно получить:

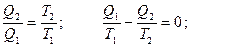(40).

Величина Q_i /T_i называется приведенной теплотой. Обозначим ее Δ S_i. Из (40) следует, что сумма приведенных теплот при циклическом процессе равна нулю. Это оз­начает, что, какой бы циклический процесс мы ни совершали, если мы вернулись в исходное состояние, некоторая величина S не меняется ( Δ S = 0). Следовательно, S – функция состояния. Она получила название энтропии. Таким образом, состояние оп­ределяется не только внутренней энергией U, но и энтропией S. Если процесс не циклический и тело переходит из состояния 1 в другое состояние 2, то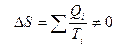. Когда тело получает теплоту (Q > 0), его энтропия возрастает, когда теряет (Q < 0) – энтро­пия уменьшается. При адиабатическом процессе (Q = 0) ΔS = 0 и S=const, поэтому адиабатический процесс называют еще изоэнтропийным.

Рассмотрим теплопередачу при контакте двух тел при температурах Т₁ и Т₂ (Т₁ > Т₂) в теплоизолированной системе. Теплота Q, передаваемая телом 1, равна теплоте Q, полученной телом 2. Однако, тело 1 отдает ее при температуре Т₁ и 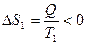, а тело 2 получает ее при температуре Т₂ и 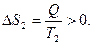Так как Т₁ > T₂, следовательно, ‌‌│Δ S ₂│>│Δ S ₁│, так что в целом при таком процессе энтропия возраста­ет. Т.о., при необратимых процессах энтропия увеличивается.

В тепловой машине часть теплоты, взятой от нагревателя, преобразуется в работу, а другая часть должна быть передана холодильнику. Нагреватель охлаждает­ся, а холодильник нагревается.

С одной стороны, мы знаем, что при этом энтропия воз­растает. С другой стороны, к.п.д. такой тепловой машины будет постепенно падать, так как и при Т₁ → T₂ к.п.д. η → 0. Общая энергия системы, включающей нагреватель, холодильник, рабочее вещество и тело, над которым производится работа, ос­тается неизменной, но работы получается все меньше и меньше. В пределе, когда Т₁ = T₂, теплота от нагревателя не может быть использована вовсе. Тогда внутренняя энергия нагревателя ста­новится бесполезной. Таким образом, возрастание энтропии со­ответствует обесцениванию энергии.

Энтропию можно связать со степенью упорядоченности си­стемы. Увеличение энтропии соответствует увеличе­нию беспорядка. Энтропия – это мера беспорядка. В наших примерах (рис.) система переходила из ме­нее вероятного, упорядоченного, неравновесного состояния в более вероятное, неупорядоченное, равновесное.

Вычислим изменение энтропии для идеального газа, исходя из дифференциальных выражений для изменения энтропии и I начала термодинамики:

dS=δQ / T; 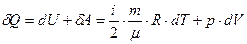(41)

Учитывая, согласно уравнению Клапейрона, что 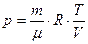, и подставив p в δ Q, а δ Q в выражение для d S, получим:

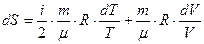, которое после интегрирования определяет изменение энтропии идеального газа при переходе от состояния 1 с Т ₁ и V ₁ к состоянию 2 с Т ₂ и V ₂: (42).

Дата добавления: 2013-12-12