
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для самостоятельного изучения
|
|
|
|
Где
ГЛАВА 4. ЗАКОНЫ СОХРАНЕНИЯ.
Задание для самоконтроля знаний.
- Определить работу и мощность силы тяжести тела массой 1 кг на всем пути его движения, если оно было брошено вертикально вверх со скоростью 10 м/с.
- Определить кинетическую энергию и импульс Земли движущуюся по орбите вокруг Солнца.
- Определить потенциальную энергию взаимодействия Земли и Луны.
- Определить модуль и направление силы действующую на тело в гравитационном поле Земли, если его потенциальная энергия уменьшается на 10 Дж при каждом миллиметре его пути.
- Определить работу силы натяжения ремня Т=100Н при вращении вала R=0,2 м, если он в момент времени t=1cот начала движения имеет угловую скорость
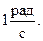
- Определить массу движущегося по горизонтальной поверхности диска R=0,2 м, если при угловой скорости ω = 2 рад/с он имеет полную энергию 100 Дж.
- Определить энергию затухающих колебаний с β=2
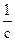 в момент времени t=1мин., когда его амплитуда была 10см при коэффициенте к=100 Н/м.
в момент времени t=1мин., когда его амплитуда была 10см при коэффициенте к=100 Н/м. - Определить добротность колебательной системы, если она имеет коэффициент затухания 2с-1, и частоту свободных колебаний π рад/с.
Лекция 6
4.1 Закон сохранения импульса
Тело массой m движущееся со скоростью 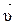 имеет импульс
имеет импульс
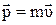 .
.
Согласно второму закону Ньютона
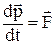 ,
,
где 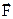 - равнодействующая сила.
- равнодействующая сила.
Если 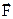 =0, то
=0, то 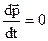 , что возможно только при
, что возможно только при 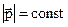 . Следовательно, импульс тела остаётся постоянным, если на него не действуют силы или их равнодействующая рана нулю.
. Следовательно, импульс тела остаётся постоянным, если на него не действуют силы или их равнодействующая рана нулю.
Рассмотрим взаимодействие двух тел, составляющих замкнутую систему (рис 4.1). Замкнутой системой называется такая система тел, в которой действует только внутренние силы f взаимодействия между телами. Для каждого тела этой системы импульс сил взаимодействия
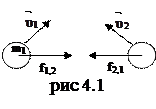
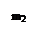
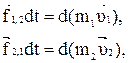 (4.1)
(4.1)
где 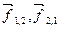 – внутренние силы, действующие на первое и второе тело со стороны второго и первого тела соответственно;
– внутренние силы, действующие на первое и второе тело со стороны второго и первого тела соответственно; 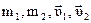 - массы и скорости взаимодействующих тел.
- массы и скорости взаимодействующих тел.
Из третьего закона Ньютона следует, что
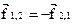 .
.
Тогда сумма импульсов сил действующих на тело
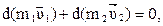
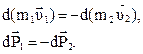 (4.2)
(4.2)
При механическом взаимодействии тел в замкнутой системе изменения их импульсов попарно равны по величине и противоположны по направлению. Изменение суммарного импульса системы 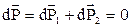 . Последнее равенство возможно, когда
. Последнее равенство возможно, когда 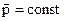 . Импульс замкнутой системы тел не изменяется с течением времени и называется законом сохранения импульса. Из закона сохранения импульса следует, что в замкнутой системе, состоящей из n тел, их векторные суммы импульсов до и после взаимодействия равны:
. Импульс замкнутой системы тел не изменяется с течением времени и называется законом сохранения импульса. Из закона сохранения импульса следует, что в замкнутой системе, состоящей из n тел, их векторные суммы импульсов до и после взаимодействия равны:
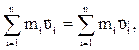 (4.3)
(4.3)
где 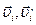 – скорость i тела до и после взаимодействия.
– скорость i тела до и после взаимодействия.
Для двух тел, при взаимодействии которых внешние силы отсутствуют или они скомпенсированы, закон сохранения импульса запишем в виде
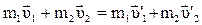 . (4.4)
. (4.4)
Для замкнутой системы из n тел импульс 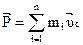 остается постоянной. Следовательно, остается постоянной и скорость центра инерции. В этом случае, центр инерции либо остается неподвижным, либо движется равномерно и прямолинейно относительно некоторой инерциальной системы отчета.
остается постоянной. Следовательно, остается постоянной и скорость центра инерции. В этом случае, центр инерции либо остается неподвижным, либо движется равномерно и прямолинейно относительно некоторой инерциальной системы отчета.
4.2 Закон сохранения момента импульса
Вращательное движение отдельного тела определятся уравнениями
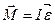 ,
, 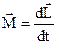 ,
,
где 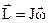 - момент импульса тела в плоскости относительно некоторой точки О через которую проходит ось вращения Z(рис 4.2).
- момент импульса тела в плоскости относительно некоторой точки О через которую проходит ось вращения Z(рис 4.2).
Модуль момента импульса материальной точки.
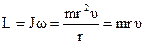 .
.
Учитывая, что 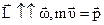 , а
, а 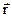 - есть радиус вектор, соединяющий точку О с центром инерции тела, то можно записать
- есть радиус вектор, соединяющий точку О с центром инерции тела, то можно записать
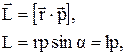
где 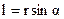 - плечо вектора
- плечо вектора 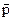 относительно точки О.
относительно точки О.
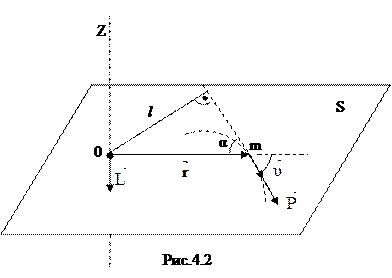
Вектор 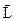 направлен вдоль оси Z и совпадает с поступательным движением правого винта (буравчика), если он вращается от вектора
направлен вдоль оси Z и совпадает с поступательным движением правого винта (буравчика), если он вращается от вектора 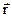 к
к 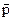 по кратчайшему пути.
по кратчайшему пути.
Закон сохранения момента импульса отдельного тела определяется из соотношения
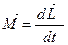 .
.
Если 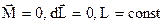 .
.
Если результирующий момент M всех внешних сил, действующих на тело, равен нулю, то момент импульса тела остаётся постоянным.
Рассмотрим систему из двух материальных точек вращающихсяв плоскости S вокруг оси проходящей через точку О взаимодействующих между собой и с внешними телами (рис 4.3)
. 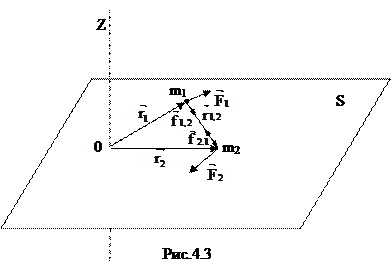
В произвольный момент времени t моменты импульсов этих тел 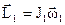 ,
, 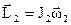 .
.
Изменение момента импульса каждого из тел обусловлено действием как внутренних, так и внешних моментов сил 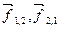
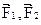 .
.
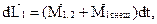
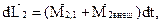
где 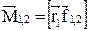 ,
, 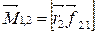 ,
,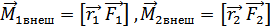 .
.
Изменение момента импульса системы тел
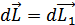 +
+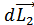 =
=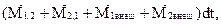 (4.5)
(4.5)
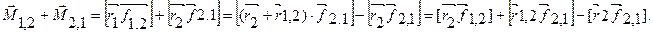 При составлении равенства (4.5) учтено, что
При составлении равенства (4.5) учтено, что 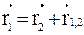 и
и 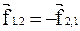 .
.
Так как 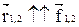 и векторное произведение двух параллельных векторов
и векторное произведение двух параллельных векторов 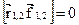 , то
, то 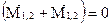 , и
, и
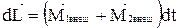 (4.6)
(4.6)
Рассмотрим два случая:
1)если суммарный момент внешних сил 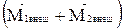 =0 (система замкнутая)
=0 (система замкнутая) 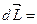 0,
0, 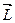 =const.
=const.
2)если система не является замкнутой, то 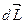 =
=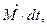
где 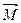 -суммарный момент всех внешних сил, действующих на систему.
-суммарный момент всех внешних сил, действующих на систему.
В замкнутой системе геометрическая сумма моментов импульсов тел всегда остается постоянной
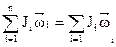 , (4.7)
, (4.7)
где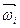 - угловая скорость вращения i-го тела системы в момент времени t.
- угловая скорость вращения i-го тела системы в момент времени t.
4.3 Закон сохранения энергии
Движущаяся система тел обладает кинетической энергией. Изменение кинетической энергии может быть обусловлено работой как консервативных Fконс, так и неконсервативных сил Fнеконс:
dEк = Aконс + Анеконс.
Работа, совершаемая консервативными и не консервативными силами
Aконс = – dEп,
Анеконс= dEк + dEп= d(Eк + Eп). (4.8)
Изменение полной механической энергии обусловлено работой только неконсервативных сил.
Если на систему действуют только консервативные силы, то Анеконс=0 а полная механическая энергия остаётся постоянной (dE=0, E=const).
В замкнутой консервативной системе, в которой взаимодействие с внешними телами отсутствует, могут происходить лишь взаимные превращения кинетической и потенциальной энергии. При этом убыль кинетической энергии всегда равна приращению потенциальной и наоборот.
Если внутри замкнутой системы действуют неконсервативные силы, например силы трения, то механическая энергия такой системы уменьшается, превращаясь в другие, немеханические виды энергии. Мерой этого превращения является работа, совершаемая неконсервативными силами.
Если система не замкнута и не консервативна, то изменение полной механической энергии при ее переходе из одного механического состояния в другое равно алгебраической сумме работ всех внешних и внутренних неконсервативных сил, действующих на систему в процессе этого перехода.
4.4.1. Применение законов сохранения к упругому и неупругому соударению двух тел.
При соударении тела деформируются. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел.
 Столкновения могут быть упругими и неупругими. Их предельные идеализированные случаи – абсолютно упругий и абсолютно неупругий удар.
Столкновения могут быть упругими и неупругими. Их предельные идеализированные случаи – абсолютно упругий и абсолютно неупругий удар.
При абсолютно упругом ударе (например, столкновении шаров из слоновой кости или закаленной стали) механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия тел полностью или частично переходит в потенциальную энергию упругой деформации. По завершении удара первоначальная форма тел полностью восстанавливается. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию и тела разлетаются со скоростями, величина и направление которых определяются законом сохранения механической энергии и законом сохранения полного импульса системы тел.
Пpи неупругом ударе (например столкновении шаров из воска, двух разноименных ионов с образованием молекулы, захвате свободного электрона положительным ионом и т.д.) тела не восстанавливают свою первоначальную форму, кинетическая энергия тел частично или полностью превращается во внутреннюю энергию. При абсолютно неупругом ударе тела движутся после удара как единое целое с одинаковой скоростью или покоятся. При абсолютно неупругом ударе закон сохранения механической энергии не соблюдается. Выполняется лишь закон сохранения импульса и закон сохранения суммарной энергии различных видов – механической и внутренней.
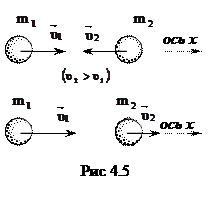
Рассмотрим случай центрального соударения двух однородных шаров. Удар называется центральным, если шары до удара движутся вдоль прямой, соединяющей их центры (рис 4.12).
Поскольку удар упругий, то механическая энергия не переходит в другие виды энергии а кинетическая энергия сохраняется:
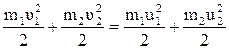 , (4.9)
, (4.9)
где 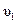 ,
, 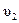 ,
, 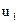 ,
, 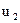 – скорости шаров до и после удара.
– скорости шаров до и после удара.
Потенциальная энергия при упругом столкновении шаров не меняется закон сохранения импульса:
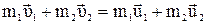 , (4.10)
, (4.10)
Уравнения (4.9) следует:
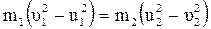 ,
,
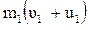
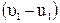 =
=
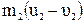
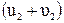 . (4.11)
. (4.11)
Из уравнения (4.10) с учетом проекции скоростей на ось Х:
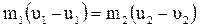 . (4.12)
. (4.12)
Поделив левые и правые части уравнении (4.11) 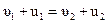 (4.12), получим:
(4.12), получим:
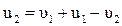
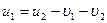 (4.13)
(4.13)
Подставим (4.13) в (4.12):
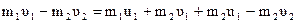 ,
,
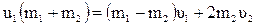 .
.
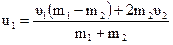 . (4.14)
. (4.14)
По аналогии, подставим в формулу (4.13) полученное значение для 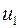 :
:
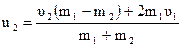 . (4.15)
. (4.15)
Рассмотрим частные случаи.
1) Массы шаров равны 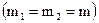 .
.
|
|
|
|
|
Дата добавления: 2013-12-11; Просмотров: 358; Нарушение авторских прав?; Мы поможем в написании вашей работы!