
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоремы существования в теории пределов последовательностей
|
|
|
|
Таблица основных эквивалентностей
=.
(вывод будет дан на одной из ближайших лекций).
При выполнении условия  имеют место следующие эквивалентности:
1. имеют место следующие эквивалентности:
1. 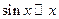 ; 2. ; 2. 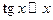 ; 3. ; 3.  ; 4. ; 4.  ; 5. ; 5.  6.
6. 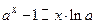 ; 7. ; 7. 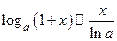 ; ;
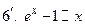 ; ; 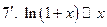 ; 8. ; 8.  . .
|
Теорема 1. ( Теорема Вейерштрасса о пределе монотонной последовательности). В пространстве 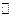 всякая возрастающая и ограниченная сверху последовательность
всякая возрастающая и ограниченная сверху последовательность 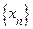 имеет конечный предел
имеет конечный предел 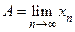 . При этом
. При этом 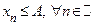 . (Убывающая ограниченная снизу последовательность имеет предел, который не превосходит всех членов последовательности.)
. (Убывающая ограниченная снизу последовательность имеет предел, который не превосходит всех членов последовательности.)
Доказательство. Достаточно рассмотреть случай возрастающей последовательности 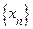 . Согласно принципу ТВГ существует
. Согласно принципу ТВГ существует 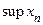 . Обозначим
. Обозначим 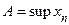 и докажем, что
и докажем, что 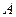 и есть предел рассматриваемой последовательности. Если
и есть предел рассматриваемой последовательности. Если 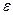 − произвольное положительное число, то
− произвольное положительное число, то  уже не является ТВГ. Поэтому найдётся номер
уже не является ТВГ. Поэтому найдётся номер 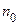 , для которого
, для которого  . В таком случае
. В таком случае  . Это значит
. Это значит 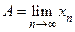 . С другой стороны, при всех
. С другой стороны, при всех 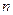
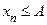 , т.к. А − ТВГ данной последовательности.
, т.к. А − ТВГ данной последовательности.
Теорема 2. (Принцип вложенных отрезков.) В пространстве 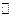 у последовательности вложенных стягивающихся отрезков имеется единственная общая точка. Более подробно. Пусть
у последовательности вложенных стягивающихся отрезков имеется единственная общая точка. Более подробно. Пусть 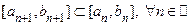 и пусть
и пусть 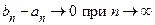 . В таком случае пересечение всех данных отрезков состоит из единственной точки
. В таком случае пересечение всех данных отрезков состоит из единственной точки 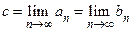 .
.
Доказательство. По условию 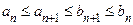 . Отсюда следует, что последовательность
. Отсюда следует, что последовательность 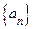 возрастает и ограничена сверху числом
возрастает и ограничена сверху числом  , а последовательность
, а последовательность  убывает и ограничена снизу числом
убывает и ограничена снизу числом 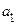 . По теореме Вейерштрасса существуют пределы
. По теореме Вейерштрасса существуют пределы 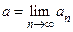 и
и  , кроме того,
, кроме того, 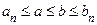 при всех
при всех 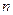 . Пересечение всех отрезков
. Пересечение всех отрезков  содержит отрезок
содержит отрезок 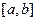 и, следовательно, непусто. Осталось доказать, что это пересечение состоит из единственной точки. Предположим, что
и, следовательно, непусто. Осталось доказать, что это пересечение состоит из единственной точки. Предположим, что  и
и 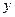 принадлежат рассматриваемому пересечению и
принадлежат рассматриваемому пересечению и 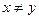 . Тогда будет
. Тогда будет  , следовательно,
, следовательно,  . И мы приходим к противоречию.
. И мы приходим к противоречию.
Теорема 3. (Теорема Больцано-Вейерштрасса). В пространстве 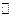 из всякого бесконечного ограниченного множества можно выделить сходящуюся последовательность.
из всякого бесконечного ограниченного множества можно выделить сходящуюся последовательность.
Доказательство. Пусть 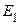 − указанное множество. Так как
− указанное множество. Так как 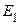 − ограниченное множество, то оно размещается на некотором отрезе
− ограниченное множество, то оно размещается на некотором отрезе 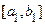 . Выберем произвольным образом
. Выберем произвольным образом 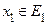 . Ясно, что
. Ясно, что  . Обозначим
. Обозначим  . Хотя бы одна из двух половинок отрезка
. Хотя бы одна из двух половинок отрезка 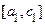 или
или 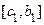 содержит бесконечное подмножество
содержит бесконечное подмножество  множества
множества 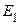 . Обозначим такую половинку
. Обозначим такую половинку 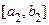 . Так как
. Так как  − бесконечное множество, то можно выбрать
− бесконечное множество, то можно выбрать  ,
, 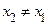 .
.
Продолжая это построение далее, получим с помощью ММИ последовательность вложенных отрезков  , последовательность бесконечных подмножеств
, последовательность бесконечных подмножеств 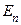 и последовательность попарно различных точек
и последовательность попарно различных точек 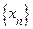 таких, что
таких, что 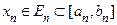 и
и 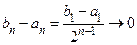 , когда
, когда  . По теореме 2 существует
. По теореме 2 существует 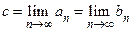 . Так как
. Так как 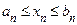 , то по теореме о двусторонней оценке
, то по теореме о двусторонней оценке  .
.
Определение. Последовательность 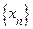 называется фундаментальной, если выполнено условие Коши:
называется фундаментальной, если выполнено условие Коши: 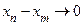 , когда
, когда 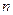 и
и  , а это значит, что
, а это значит, что 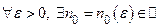 :
: 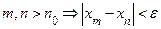 .
.
Легко видеть, что всякая сходящаяся последовательность фундаментальна. Действительно, если 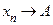 , когда
, когда  , то
, то 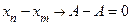 , при условии, что
, при условии, что 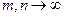 . (Заметим, что на множестве
. (Заметим, что на множестве 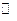 обратное утверждение не верно. Так, например, последовательность рациональных чисел, сходящаяся к иррациональному числу, фундаментальна, но
обратное утверждение не верно. Так, например, последовательность рациональных чисел, сходящаяся к иррациональному числу, фундаментальна, но 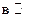 у неё нет предела.)
у неё нет предела.)
Теорема 4. (Критерий Коши сходимости последовательностей). В 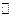 последовательность является сходящейся, тогда и только тогда, когда эта последовательность фундаментальна.
последовательность является сходящейся, тогда и только тогда, когда эта последовательность фундаментальна.
Необходимость условия Коши уже доказана. Для доказательства достаточности понадобятся 2 леммы.
Лемма 1. Фундаментальная последовательность ограниченна.
Доказательство. Пусть  . Тогда
. Тогда 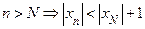 . Если
. Если 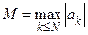 , то
, то  при всех
при всех 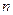 .
.
Лемма 2. Если фундаментальная последовательность содержит сходящуюся подпоследовательность, то вся последовательность тоже является сходящейся.
Доказательство. Пусть 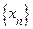 − фундаментальная последовательность и
− фундаментальная последовательность и  . Для любого положительного числа
. Для любого положительного числа 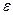 можно указать такой номер
можно указать такой номер 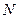 , после которого будут выполнены оба следующих условия
, после которого будут выполнены оба следующих условия  . В таком случае, при всех
. В таком случае, при всех 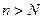 будем иметь
будем иметь 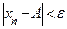 . Это и означает, что последовательность
. Это и означает, что последовательность 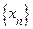 сходится и её предел равен
сходится и её предел равен 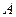 .
.
Доказательство достаточности условия Коши. Пусть 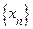 − фундаментальная последовательность. По лемме 1 эта последовательность ограничена. Теорема Больцано-Вейерштрасса показывает, что из нее можно выделить сходящуюся подпоследовательность
− фундаментальная последовательность. По лемме 1 эта последовательность ограничена. Теорема Больцано-Вейерштрасса показывает, что из нее можно выделить сходящуюся подпоследовательность 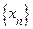 . Но тогда из леммы 2 следует, что последовательность
. Но тогда из леммы 2 следует, что последовательность 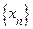 является сходящейся.
является сходящейся.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1071; Нарушение авторских прав?; Мы поможем в написании вашей работы!