
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод математической индукции. Неравенство Я. Бернулли
|
|
|
|
Напомним известную забаву. Кости домино выставляются таким образом, что каждая из них падая, опрокинет следующую кость. Если толкнуть первую, то одна за другой упадут все кости. Принцип математической индукции формулируется сходным образом. Рассмотрим применение метода математической индукции (ММИ) на примере.
Пример 1. Сумма членов арифметической прогрессии 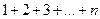 равна
равна  .
.
Рассмотрим похожую сумму 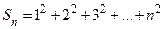 . Доказать равенство
. Доказать равенство 
(утверждение 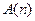 ).
).
Решение. Утверждение 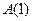 истинно, т.к. при
истинно, т.к. при 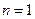 Л.ч.=П.ч.=1.
Л.ч.=П.ч.=1.
Докажем, что  . Если
. Если  , то.
, то.
 =
= , т.е.
, т.е. 
Таким образом,  .
.
Формулировка принципа математической индукции:
Пусть 1) 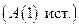 − база индукции;
2) − база индукции;
2)  − шаг индукции.
Тогда − шаг индукции.
Тогда 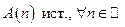 . .
|
Упражнение. Доказать, что  .
.
Пример 2. Доказать неравенство Бернулли: если  , то
, то 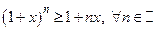 (утверждение
(утверждение 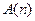 ).
).
Доказательство. 1) 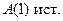 , т.к. при
, т.к. при 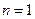 Л.ч.=Пр.ч.=1+ x
Л.ч.=Пр.ч.=1+ x
2) Пусть  , т.е.
, т.е. 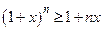 при
при  . Домножим обе части этого неравенства на величину
. Домножим обе части этого неравенства на величину  . Т.к.
. Т.к.  , то мы получим
, то мы получим  .
.
Таким образом,  , т.е.
, т.е.  истинно.
истинно.
Мы доказали, что 1) 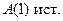 и 2)
и 2)  . В соответствии с принципом математической индукции
. В соответствии с принципом математической индукции  . Ч. и т.д.
. Ч. и т.д.
Замечание. Из приведенного доказательства следует также, что, если  , в неравенстве Бернулли знак “
, в неравенстве Бернулли знак “ ” можно заменить знаком “
” можно заменить знаком “ ”.
”.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1188; Нарушение авторских прав?; Мы поможем в написании вашей работы!