
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Затухающие колебания. В условиях, когда на тело действует только одна квазиупругая сила, оно будет совершать незатухающие гармонические колебания с постоянной амплитудой A = const
|
|
|
|
В условиях, когда на тело действует только одна квазиупругая сила, оно будет совершать незатухающие гармонические колебания с постоянной амплитудой A = const. На реально же движущиеся nела всегда будут воздействовать со стороны окружающей среды силы трения, препятствующие их движению. На преодоление сопротивления среды и т.п. будет затрачиваться энергия. Вследствие этого механическая энергия колеблющегося тела будет непрерывно уменьшаться, переходя в другие формы энергии и рассеиваясь в окружающую среду. С уменьшением энергии колебания будет уменьшаться его амплитуда, и колебание станет затухающим. Полная сила F, действующая на колеблющуюся точку, будет тогда суммой квазиупругой силы F кв–упр и силы трения F тр. При малых скоростях движения сопротивление обычно пропорционально первой степени скорости и направлено противоположно ей, т.е.
F тр= – rv = – r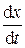 ,
,
где r — коэффициент трения, зависящий от свойств среды, формы и размеров движущегося тела.
На основании 2 закона Ньютона получим дифференциальное уравнение одномерного движения материальной точки массы m под действием квазиупругой силы и силы трения
m = – r
= – r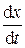 – kx.
– kx.
m + r
+ r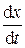 + kx. = 0.
+ kx. = 0.
Решение данного дифференциального уравнения имеет вид:
x = A 0 e–at cos(wt + j 0)

где a =  – коэффициент затухания – физическая величина, обратная промежутку времени t (время релаксации), в течение которого амплитуда убывает в е раз;
– коэффициент затухания – физическая величина, обратная промежутку времени t (время релаксации), в течение которого амплитуда убывает в е раз;
w = =
=  – циклическая частота затухающих колебаний,
– циклическая частота затухающих колебаний,
w 0 – циклическая частота собственных колебаний точки при отсутствии трения.
Чем больше коэффициент трения r, тем больше величина α в показателе степени и тем быстрее амплитуда затухающих колебаний убывает со временем.
При наличии трения не только убывает со временем амплитуда колебания, но и уменьшается угловая частота колебаний.
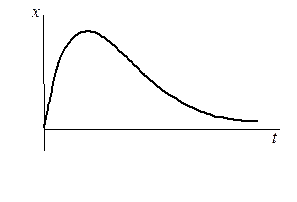 С увеличением трения период колебаний возрастает, и при r = 2 m w 0,т.е. a = w 0 период становится бесконечным (Т = ∞). При дальнейшем увеличении a период Т становится мнимым, а движение точки – апериодическим.
С увеличением трения период колебаний возрастает, и при r = 2 m w 0,т.е. a = w 0 период становится бесконечным (Т = ∞). При дальнейшем увеличении a период Т становится мнимым, а движение точки – апериодическим.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 519; Нарушение авторских прав?; Мы поможем в написании вашей работы!