Вынужденные колебания. Резонанс

Для получения незатухающих колебаний необходимо воздействие дополнительной переменной внешней силы, которая подталкивала бы точку то в одну, то в другую сторону и работа которой непрерывно восполняла бы убыль энергии, затрачиваемой на преодоление трения. Подобная переменная сила называется вынуждающей (F _вын), а возникающие под ее действием незатухающие колебания – вынужденными.

Разберем простейший случай вынуждающей силы, меняющейся по закону синуса или косинуса, т.е. положим

F _вын = F ₀ cos(W t)

где F ₀ – есть амплитуда вынуждающей силы, W – угловая частота колебаний вынуждающей силы.

Полная сила, действующая на колеблющуюся точку, будет алгебраической суммой квазиупругой силы, силы трения и вынуждающей силы, и дифференциальное уравнение движения примет вид

m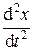 = – r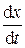 – kx + F ₀ cos(W t),

решение этого уравнения

x (t) = x _своб(t) + x _вын(t),

представляет собой сумму свободных колебаний x _своб(t)и вынужденных колебаний x _вын(t). Свободные колебания будут происходить с собственной угловой частотой w = и быстро затухнут, а частота вынужденных колебаний совпадает с частотой вынуждающей силы. Амплитуда этих колебаний должна быть постоянной, поскольку амплитуда вынуждающей силы не меняется со временем. Поэтому, собственными колебаниями системы, играющими существенную роль лишь в самом начале процесса, можно пренебречь.

Тогда решение уравнения будет иметь вид

x (t) = x _вын(t)= А cos(W t + Ф),

где А = 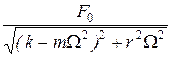– амплитуда вынужденных колебаний,

Ф = arctg – сдвиг фазы

x _вын(t)не зависит от начальных условий движения, когда в силу затухания x _своб(t)обратится в нуль, колебательное движение будет определяться только свойствами колеблющейся системы и амплитудой и частотой вынуждающей силы.

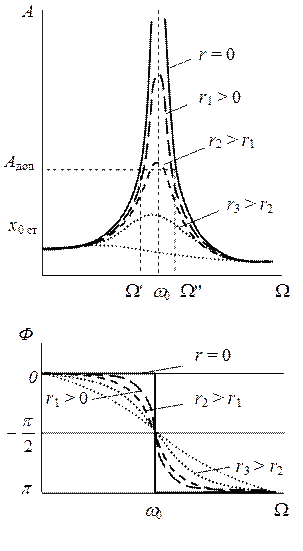
Под действием периодической вынуждающей силы F _вын возникают гармонические вынужденные колебания с частотой W. Амплитуда вынужденных колебаний А прямо пропорциональна амплитуде вынуждающей силы F ₀,зависит от характеристик свободно колеблющейся точки т, k и r и является функцией угловой частоты колебаний вынуждающей силы W. Графики зависимости А и сдвига фаз Ф от W (для нескольких значений r) представлены на рисунке.

Как видно из этих графиков, характер этих зависимостей различен в трех областях изменения угловой частоты W.

1) область малых частот:

В этой области сдвиг фаз Ф близок к нулю, а выражение для амплитуды можно преобразовать к виду

В предельном случае, когда W = 0 (при постоянной нагрузке),

А = 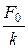= x _0ст,

где x _{0 ст} – статическое смещение точки под действием постоянной силы F = F ₀. При 0 < W << ω ₀ и малом трении (a << w ₀) получим

x ≈ cosW t =

т.е. смещение колеблющейся точки почти без искажений следует за изменением вынуждающей силы. Этот случай представляет практический интерес для измерительной техники.[3]

2) область высоких частот:

При таких частотах Ф ≈ – p и колебания точки происходят в фазе, противоположной колебаниям вынуждающей силы. Когда смещение положительно, вынуждающая сила отрицательна, и наоборот. Вследствие этого амплитуда вынужденных колебаний не может быть большой и убывает с ростом частоты вынуждающей силы по закону

A = x _{0 ст}

Подобный случай также имеет важное практическое значение.[4].

3) область резонанса:

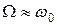
При частотах колебания вынуждающей силы, близких к частоте собственных колебаний системы, амплитуда вынужденных колебаний сильно возрастает и начинает во много раз превышать статическое смещение:

A ≈ x _{0 ст}

Чем меньше коэффициент трения, тем больше эта амплитуда. В пределе, А → ∞ при r → 0. Это явление резкого возрастания амплитуды вынужденных колебаний при W ≈ w ₀ носит название механического резонанса.

Явления резонанса широко распространены в природе и технике[5].

[1] Когда речь идет только о линейных скоростях и другие скорости (угловые) не рассматриваются, термин «линейная» обычно опускается.

[2] Существует три понятия, имеющие одинаковое название: масса, как мера инертности; масса, как мера количества вещества; масса, как мера гравитационного взаимодействия. Однако численного различия между ними не установлено.

[3] Различные самопишущие приборы для регистрации быстропеременных усилий (например, мембранный индикатор, записывающий давление в быстроходном двигателе) представляют собой системы, на которые действуют упругие или квазиупругие силы, возвращающие систему в положение равновесия после снятия нагрузки. Переменное усилие является для такой системы вынуждающей силой со своей характерной угловой частотой W (или несколькими угловыми частотами W _i). Чтобы вынужденные колебания прибора успевали следовать за изменениями вынуждающей силы, собственная частота колебаний прибора ω ₀ должна быть во много раз больше частоты изменения измеряемой величины Ω. При ω ₀ > 10W ошибка измерений не будет превышать 1–2%. Увеличение собственной частоты ω ₀ достигается как за счет увеличения жесткости измерительной системы k, так и за счет уменьшения ее массы т (с ростом k и уменьшением т величина tg Ф → 0, а следовательно, и сдвиг фаз Ф → 0)

[4] Например, для предотвращения воздействия качки корабля на различные приборы их следует подвешивать на сравнительно мягких пружинах и максимально утяжелять. Если при этом частота собственных колебаний системы w ₀ будет сделана много меньше частоты качки W, то амплитуда колебаний подвешенного прибора будет много меньше амплитуды колебаний точки подвеса.

[5] Когда войсковая часть идет по мосту, то обязательно подается команда идти «не в ногу». Периодические толчки, создаваемые строем солдат при ходьбе «в ногу», могут попасть в резонанс с собственными колебаниями моста и привести к его разрушению. Маломощный двигатель, если он плохо уравновешен и при вращении «бьет», может в случае резонанса разрушить или сильно повредить сооружение, на котором он укреплен, и т.п

С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если частота их совпадает с частотой собственных колебаний прибора. Вся прикладная акустика и радиотехника, аппараты, воспринимающие звуковые и электрические колебания, основаны на явлениях резонанса. Возможность поддерживать незатухающие колебания представляет чрезвычайный интерес для техники. Особенно важными и широко применяемыми являются колебательные движения, возникающие и поддерживающиеся за счет постоянного, неколебательного источника энергии. Такие системы называются автоколебательными. В качестве примеров автоколебательных систем можно привести: часы, в которых постоянные колебания маятника поддерживаются за счет энергии спиральной пружины или поднятого груза; радиопередатчик, энергия колебаний которого поддерживается за счет энергии аккумуляторных батарей; электрический звонок, пневматический молоток и многие другие приборы.

Чтобы колебательное движение не затухало, к колеблющейся системе необходимо подводить энергию для компенсации ее потерь в процессе колебаний. Подвод энергии осуществляется в виде «толчков» в подходящие моменты времени. Толчок должен ускорить, а не замедлить колебание. В автоколебательной системе включение источника энергии для получения нужного толчка производится самой системой, что гарантирует получение толчков в нужные моменты времени.

В 20 веке открыт новый тип резонанса, получивший название параметрического резонанса. Представим себе, что одна из физических величин («параметров»), определяющая свойства колебательной системы, сама периодически меняется. Таким параметром в случаях маятника или качелей может быть расстояние от оси колебаний до центра инерции системы.

При наличии малых колебаний системы периодическое изменение такого параметра может, при соответствующей частоте, привести к значительному усилению колебаний – это и есть параметрический резонанс.

Если качели совершают малые колебания, то эти колебания можно усилить, поднимаясь и приседая в «такт», т.е. меняя положение центра инерции системы относительно оси колебаний

Дата добавления: 2013-12-13