ЛЕКЦИЯ 11. Гармонические колебания. Физический маятник

Гармонические колебания. Физический маятник.

Периодическое движение – через равные промежутки времени (период ) движение повторяется.

Гармоническое колебание материальной точки – координата точки изменяется по гармони-ческому закону

.

Здесь 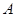- амплитуда колебания, 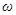- круговая (циклическая) частота, , 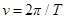- частота, 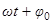- фаза колебания, 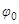- начальная фаза.

Скорость материальной точки, совершающей гармоническое колебание:

.

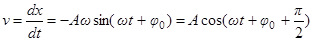Исходя из этого выражения, можно говорить, что при гармоническом колебании скорость опережает по фазе координату на .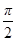

Ускорение колебательного движения:

.

Таким образом, мы приходим к уравнению осциллятора

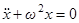, (1)

составляющему основу теории колебаний (производная обозначена точками).

Собственные колебания возникают за счет собственных сил, существующих в самой системе. Частота таких колебаний называется собственной частотой.

Пример. Пружинный маятник.

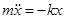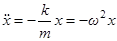, . Значит собственная частота , .

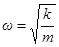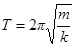Полная энергия материальной точки при гармонических колебаниях:

.

Средние за период значения кинетической и потенциальной энергии:

, .

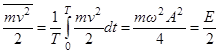Таким образом, при гармонических колебаниях

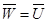(частный случай общей теоремы вириала).

Математический маятник – тело, подвешенное на невесомой нерастяжимой нити, размер которого намного меньше длины нити.

Физический маятник – тело, закрепленное на оси, расположенной выше центра масс.

Основной закон вращательного движения для такого тела

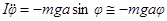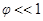(). Преобразуем его к виду (1)

.

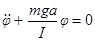Тогда 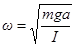, - период колебаний физического маятника.

Если размеры тела малы по сравнению с расстоянием 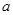(материаль-ная точка), то 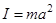и мы приходим к известной формуле для периода математического маятника

.

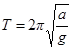Приведенная длина физического маятника – это длина математического маятника с тем же периодом колебаний, что и у физического. Приравнивая выражения для периодов, получим

.

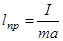Обозначим через точку, лежащую на продолжении отрезка 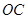и отстоящую от точки подвеса на расстоянии . Точка называется центром качаний физического маятника. Можно показать, что физический маятник обладает следующим важным свойством: если физический маятник подвесить за центр качаний, то период его колебаний не изменится.

Дата добавления: 2013-12-13